Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

có ai on ko nó chuyện vs mih chứ ai đng xem bóng đá thì cứ xem

1. Ta có ÐOMP = 900 ( vì PM ^ AB ); ÐONP = 900 (vì NP là tiếp tuyến ).
Như vậy M và N cùng nhìn OP dưới một góc bằng 900 => M và N cùng nằm trên đường tròn đường kính OP => Tứ giác OMNP nội tiếp.
2. Tứ giác OMNP nội tiếp => ÐOPM = Ð ONM (nội tiếp chắn cung OM)
Tam giác ONC cân tại O vì có ON = OC = R => ÐONC = ÐOCN
=> ÐOPM = ÐOCM.
Xét hai tam giác OMC và MOP ta có ÐMOC = ÐOMP = 900; ÐOPM = ÐOCM => ÐCMO = ÐPOM lại có MO là cạnh chung => DOMC = DMOP => OC = MP. (1)
Theo giả thiết Ta có CD ^ AB; PM ^ AB => CO//PM (2).
Từ (1) và (2) => Tứ giác CMPO là hình bình hành.
3. Xét hai tam giác OMC và NDC ta có ÐMOC = 900 ( gt CD ^ AB); ÐDNC = 900 (nội tiếp chắn nửa đường tròn ) => ÐMOC =ÐDNC = 900 lại có ÐC là góc chung => DOMC ~DNDC
=> => CM. CN = CO.CD mà CO = R; CD = 2R nên CO.CD = 2R2 không đổi => CM.CN =2R2không đổi hay tích CM. CN không phụ thuộc vào vị trí của điểm M.
.

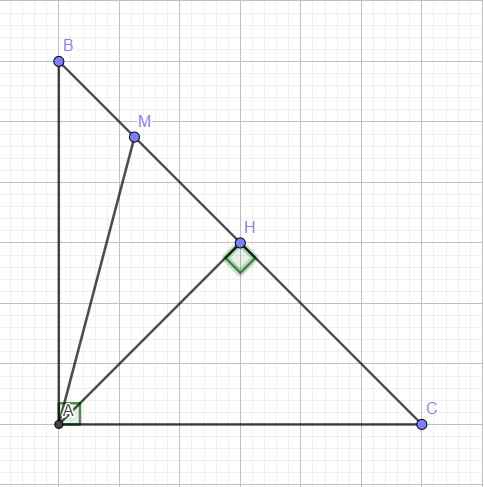
Do tính đối xứng, không mất tính tổng quát, giả sử M nằm giữa B và H
ABC vuông cân \(\Rightarrow BH=CH=AH\)
Ta có:
\(\dfrac{MA^2}{MB^2+MC^2}=\dfrac{MA^2}{\left(BH-MH\right)^2+\left(CH+MH\right)^2}=\dfrac{MA^2}{\left(BH-MH\right)^2+\left(BH+MH\right)^2}\)
\(=\dfrac{MA^2}{2\left(BH^2+MH^2\right)}=\dfrac{MA^2}{2\left(AH^2+MH^2\right)}=\dfrac{MA^2}{2MA^2}=\dfrac{1}{2}\)

Do tính đối xứng, ko mất tính tổng quát, giả sử M nằm giữa B và H
ABC vuông cân \(\Rightarrow AH\) đồng thời là trung tuyến
\(\Rightarrow AH=\dfrac{1}{2}BC\Rightarrow AH=BH=CH\)
Ta có:
\(\dfrac{MA^2}{MB^2+MC^2}=\dfrac{MA^2}{\left(BH-HM\right)^2+\left(CH+MH\right)^2}=\dfrac{MA^2}{\left(AH-MH\right)^2+\left(AH+MH\right)^2}\)
\(=\dfrac{MA^2}{2\left(AH^2+MH^2\right)}=\dfrac{MA^2}{2MA^2}=\dfrac{1}{2}\)