Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét (O;R) có:
\(\widehat{BCD}\)là góc nt chắn cung BC
\(\widehat{BAC}\)là góc nt chắn cung BC
\(\Rightarrow\widehat{BCD}=\widehat{BAC}=sđ\widebat{BC}\)
Vì dây \(AB\perp CD\)tại M nên \(\widehat{M}=90^o\)
Xét \(\Delta ACM\)và \(\Delta DBM\):
\(\hept{\begin{cases}\widehat{AMC}=\widehat{DMB}=90^o\\\widehat{BAC}=\widehat{BCD}\end{cases}}\)
\(\Rightarrow\Delta ACM\infty\Delta DBM\left(gg\right)\)
\(\Rightarrow\frac{AM}{DM}=\frac{MC}{MB}\Rightarrow AM.MB=MC.DM\)
b) Vì \(\Delta ACM\infty DBM\Rightarrow\widehat{ACM}=\widehat{DBM}\)
Xét \(\left(O;R\right):\)
\(\Delta CDE\)nt (O), cạnh DE là đường kính\(\Rightarrow\Delta CDE\)vuông tại C\(\Rightarrow CD\perp CE\Rightarrow\widehat{DCE}=90^o\)
\(\Delta BDE\)nt \(\left(O\right),\)cạnh DE là đường kính\(\Rightarrow\Delta BDE\)vuông tại B\(\Rightarrow\widehat{DBE}=90^o\)
Có\(\widehat{MAC}+\widehat{ACM}=90^o\Rightarrow\widehat{MAC}=90^o-\widehat{ACM}\)
Và \(\widehat{ABE}+\widehat{DBM}=90^o\Rightarrow\widehat{ABE}=90^o-\widehat{DBM}\)
Mà \(\widehat{ACM}=\widehat{DBM}\)\(\Rightarrow\widehat{MAC}=\widehat{ABE}\)
Do \(AB\perp CD,CD\perp CE\Rightarrow AB//CE\)
Xét tg ABCE có:
\(AB//CE\)
\(\widehat{MAC}=\widehat{ABE}\)
\(\Rightarrow Tg\)ABCE là hthang cân
c) Áp dụng đ/lí Pi-ta-go lần lượt vào các \(\Delta AMC,\Delta BCM;\Delta BDM;\Delta ADM;\Delta BDE\)có:
\(AM^2=AC^2-CM^2\)(1)
\(MB^2=BC^2-CM^2\)(2)
\(MC^2=BC^2-BM^2\)(3)
\(MD^2=BD^2-BM^2\)(4)
\(DE^2=BD^2+BE^2\)(5)
Công từng vế của (1)(2)(3)(4) ta đc đẳng thức:
\(MA^2+MB^2+MC^2+MD^2=AC^2-CM^2+BC^2-CM^2+BC^2-BM^2+BD^2-BM^2\)
\(=AC^2+2BC^2-2CM^2-BM^2+BD^2-BM^2\)
\(=AC^2+2BM^2-BM^2+BD^2-BM^2\)(vì \(BM^2=BC^2-CM^2\))
\(=AC^2+BD^2\)
\(=BE^2+BD^2\)(vì AC=BE do ABCE là hthang cân)
\(=DE^2\)(c/m (5))
Mà DE là đường kính của (O) nên DE=2R\(\Rightarrow DE^2=\left(2R\right)^2=4R^2\)
Vậy \(MA^2+MB^2+MC^2+MD^2\)có g/trị ko đổi khi M thay đổi trong (O)

Hướng dẫn thôi nha
Câu a) : Vẽ MH vuông góc với AC, MK vuông góc với BD
Ta có MA x MC = MH x AC = 2 x R x MH
Ta CM \(^{ }MA^4\)+ \(^{ }MC^4\)= \(^{ }16R^4\)- \(8^{ }R^2MH^2\)
Tương tự MB^4 + MD^4 = 16R^4 - 8R^2 x HK^2
Kq bằng \(^{ }24R^4\)
Câu b) áp dụng cô si cho 4 số kq bằng \(^{ }6R^4\)
Tick cho mình nhaaaaaaaaa :*
khó thế
mới học lớp 3 bài này khó quá anh chị cho bài về bảng nhân đi ạ 000000

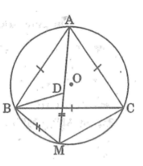
Ta có: ∆ ABD = ∆ CBM (cmt)
suy ra: AD = CM
Ta có: DM = BM ( tam giác MBD đều )
mà AM = AD + DM
suy ra: MA = MC + MB

Lười quá, chắc mình giải câu c thôi ha.
Vẽ \(OH\) vuông góc \(d\) tại \(H\). \(AB\) cắt \(OH\) tại \(L\). \(OM\) cắt \(AB\) tại \(T\)
H M A B O d L T .
CM được \(OL.OH=OT.OM=R^2\) nên \(L\) cố định. Vậy \(AB\) luôn qua \(L\) cố định.

a) Tứ giác AOBE nội tiếng ( 2 góc đối = 180 độ )
b) tam giác OMH đồng dạng tam giác OIK ( góc hóc) ==> đpcm
c) Có MI vuông góc AB, IA=IB==> tam gisc MAB cân tại M
đồng thời E cách đều AB, ==> đpcm

3: góc MHO=góc MAO=góc MBO=90 độ
=>M,A,O,H,B cùng nằm trên đường tròn đường kính OM
=>góc HAB=góc HMB
CE//MB
=>góc HCE=góc HMB=góc HAB
=>ACEH nội tiếp
=>góc CHE=góc CAE
mà góc CAE=góc CDB
nên gó CHE=góc CDB
=>HE//DB
Gọi K là giao của CE và DB
Xét ΔCKD có
H là trung điểm của CD
HE//KD
=>E là trung điểm của CK
=>EC=EK
Vì CK//MB
nên CE/MF=DE/DF=EK/FB
mà CE=EK
nên MF=FB
=>F là trung điểm của MB