Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải thích các bước giải:
Gọi cạnh hình vuông là a
Vì M là trung điểm DC →DM=12a→AM=√AD2+DM2=a√52→DM=12a→AM=AD2+DM2=a52
Ta có : AK⊥KM,AD⊥DM→ADMKAK⊥KM,AD⊥DM→ADMK nội tiếp
→ˆKAM=ˆKDM=45o→ΔKMA→KAM^=KDM^=45o→ΔKMA vuông cân tại K→AK=KM=MA√2=a√52√2→AK=KM=MA2=a522
Do ADMKADMK là tứ giác nội tiếp, theo định lý ptoleme
→AD.KM+DM.AK=AM.DK→
Gọi giao của AC và BD là O, cạnh hình vuông là AB=a
=>AC=DB=a căn 2; \(OA=OB=OC=OD=\dfrac{a\sqrt{2}}{2}\)
góc ADM=góc AKM=90 độ
=>AKMD nội tiếp
=>góc AKM=góc KDM=45 độ
=>ΔKAM vuông cân tại K
ΔADM vuông tại D
=>\(AM^2=AD^2+DM^2=\dfrac{5}{4}a^2\)
ΔAKM vuôg cân tại K
=>\(AM^2=2\cdot AK^2\)
=>\(2AK^2=\dfrac{5}{4}a^2\)
=>AK^2=5/8a^2
ΔAOK vuông tại O nên OK^2=AK^2+AO^2
=>OK=a/2căn 2
=>DK=DO+OK=3/4*a*căn 2
=>DK/DB=3/4

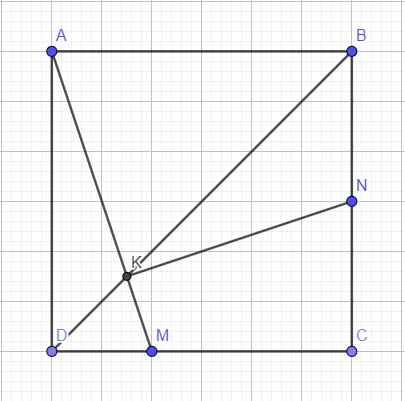
Talet: \(\dfrac{KM}{AK}=\dfrac{DM}{AB}=\dfrac{1}{3}\Rightarrow KM=\dfrac{1}{3}AK\Rightarrow KM=\dfrac{1}{4}AM\Rightarrow\overrightarrow{KM}=\dfrac{1}{4}\overrightarrow{AM}\)
Mà \(\overrightarrow{AM}=\overrightarrow{AD}+\overrightarrow{DM}=\overrightarrow{AD}+\dfrac{1}{3}\overrightarrow{AB}\Rightarrow\overrightarrow{KM}=\dfrac{1}{4}\overrightarrow{AD}+\dfrac{1}{12}\overrightarrow{AB}\)
\(\overrightarrow{KN}=\overrightarrow{KM}+\overrightarrow{MC}+\overrightarrow{CN}=\dfrac{1}{4}\overrightarrow{AD}+\dfrac{1}{12}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}\)
\(=\dfrac{3}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{KN}=\left(\overrightarrow{AD}+\dfrac{1}{3}\overrightarrow{AB}\right)\left(\dfrac{3}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AD}\right)=\dfrac{1}{4}AB^2-\dfrac{1}{4}AD^2=0\)
\(\Rightarrow AM\perp KN\Rightarrow\) đường thẳng KN nhận (10;1) là 1 vtpt
Phương trình NK:
\(10\left(x-0\right)+1\left(y-2019\right)=0\Leftrightarrow10x+y-2019=0\)
\(d\left(O;NK\right)=\dfrac{\left|-2019\right|}{\sqrt{10^2+1^2}}=\dfrac{2019}{\sqrt{101}}\)

a) Ta có góc BEC = góc BDC = 90o (góc nội tiếp chắn giữa đường tròn)
Suy ra BD \(\perp\) AC và CE \(\perp\) AB. Mà BD cắt CE tại H là trực tâm \(\Delta\) ABC.
Suy ra AH \(\perp\) BC
Vì AH \(\perp\) BC, BD \(\perp\) AC nên góc HFC = góc HDC = 90o.
Suy ra góc HFC + góc HDC = 180o
Suy ra HFCD là tứ giác nội tiếp
\(\Rightarrow\) góc HDC = góc HCD.
b) Vì M là trung điểm cạnh huyền của hình tam giác vuông ADH nên MD = MA = MH. Tương tự ta có ME = MA = MH
Suy ra MD = ME
Mà OD = OE nên \(\Delta\) OEM = \(\Delta\) ODM \(\Rightarrow\) góc MOE = góc MOD = \(\frac{1}{2}\) góc EOD
Theo qua hệ giữa góc nội tiếp và góc ở tâm cùng chắn cung, ta có góc ECD = \(\frac{1}{2}\) góc EOD
Theo ý a) ta có góc HFD = góc HCD = góc ECD
\(\Rightarrow\) góc MOD = góc HFD hay góc MOD = góc MFD
Suy ra tứ giác MFOD là tứ giác nội tiếp
\(\Rightarrow\) góc MDO = 180o - góc MPO = 90o \(\Rightarrow\) MD \(\perp\) DO
Chứng minh tương tự ta có MEFO là tứ giác nội tiếp
Suy ra 5 điểm M, E, F, O, D cùng thộc 1 đường tròn.
tớ chẳng hiểu