Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

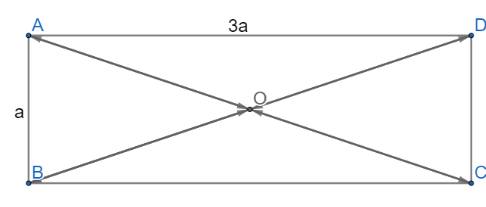
a) Ta có:
\(AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {{\left( {3a} \right)}^2}} = a\sqrt {10} \)
+) \(\left| {\overrightarrow {AC} } \right| = AC = a\sqrt {10} \)
+) \(\left| {\overrightarrow {BD} } \right| = BD = a\sqrt {10} \)
b) O là giao điểm của hai đường chéo nên ta có:
\(AO = OC = BO = OD = \frac{{a\sqrt {10} }}{2}\)
Dựa vào hình vẽ ta thấy AO và CO cùng nằm trên một đường thẳng; BO và DO cùng nằm trên một đường thẳng
Suy ra các cặp vectơ đối nhau và có độ dài bằng \(\frac{{a\sqrt {10} }}{2}\) là:
\(\overrightarrow {OA} \) và \(\overrightarrow {OC} \); \(\overrightarrow {AO} \) và \(\overrightarrow {CO} \); \(\overrightarrow {OB} \) và \(\overrightarrow {OD} \); \(\overrightarrow {BO} \) và \(\overrightarrow {DO} \)

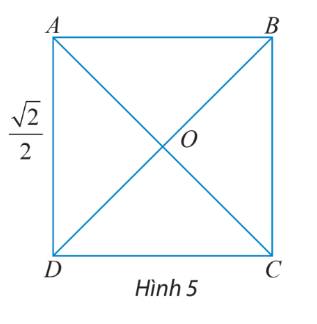
Ta có: \(AC = BD = \sqrt {A{D^2} + D{C^2}} = \sqrt {{{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2} + {{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2}} = 1\)
\(OA = \frac{1}{2}AC = \frac{1}{2}\)
Suy ra: \(\left| {\overrightarrow {AC} } \right| = 1\), \(\left| {\overrightarrow {BD} } \right| = 1\), \(\left| {\overrightarrow {OA} } \right| = 1\), \(\left| {\overrightarrow {AO} } \right| = 1\)

Từ giả thiết ta có:
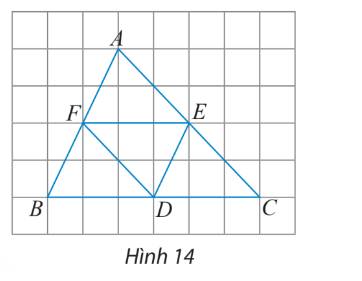
\(AF = FB = ED\); \(AE = EC = FD\); \(BD = DC = EF\)
Từ đó dựa vào hình ta có:
a) Các vectơ bằng vectơ \(\overrightarrow {EF} \)là \(\overrightarrow {DB} \) và \(\overrightarrow {CD} \)
b) Các vectơ đối vectơ \(\overrightarrow {EC} \) là \(\overrightarrow {EA} \) và \(\overrightarrow {DF} \)

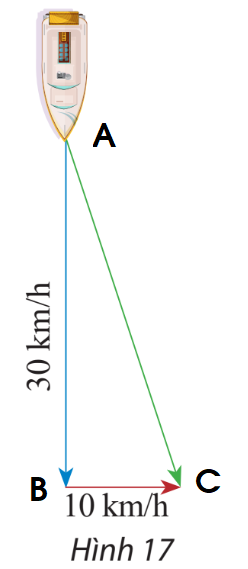
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).

Bằng \(\overrightarrow{AB}\) là \(\overrightarrow{DC}\)
Bằng \(\overrightarrow{OB}\) là \(\overrightarrow{DO}\)
Có độ dài bằng OB là \(\overrightarrow{OB};\overrightarrow{BO};\overrightarrow{OD};\overrightarrow{DO}\)
a) Bằng vectơ AB :
\(\overrightarrow{DC}\)
Bằng vectơ OB :
\(\overrightarrow{DO}\)
b)Có độ dài bằng OB :
\(\overrightarrow{OD},
\overrightarrow{DO},
\overrightarrow{BO}\)


+) ABCD là hình thoi nên cũng là hình bình hành
Áp dụng quy tắc hình bình hành ta có:
\(\overrightarrow p = \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
\(\Rightarrow |\overrightarrow p| = | \overrightarrow {AC}| =AC \)
+) \(\overrightarrow u = \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \)
\(\Rightarrow |\overrightarrow u| = | \overrightarrow {DB}| =DB\)
+) \(\overrightarrow v = 2\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {AB} + \left( {\overrightarrow {AB} - \overrightarrow {AC} } \right) = \overrightarrow {AB} + \overrightarrow {CB} \)\( = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DB} \)
\(\Rightarrow |\overrightarrow v| = | \overrightarrow {DB}| =DB\)
+ Tính \(AC, DB\)
Tam giác ABD có \(AB=AD=a, \widehat A = 60^o\) nên nó là tam giác đều. Do đó DB = a.
Gọi O là giao điểm hai đường chéo.
Ta có: \(AO = AB. \sin B = a. \sin 60^o = \frac {a \sqrt 3}{2} \Rightarrow AC = a \sqrt 3\)
Vậy \(|\overrightarrow p| = a \sqrt 3 ,|\overrightarrow u| = a, |\overrightarrow v| = a.\)

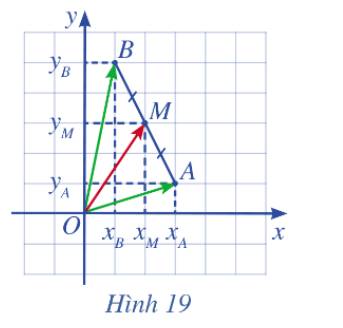
a) Ta có vectơ \(\overrightarrow {OM} \) biểu diễn theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) là: \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) Do tọa độ hai điểm A và B là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right)\)
Vậy \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left( {{x_A} + {x_B};{y_A} + {y_B}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm M chính là tọa độ của vectơ nên tọa độ M là \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)

a) I là tâm của ABCD, suy ra \(\widehat {IDC} = 45^\circ \)
b) Vectơ có điểm đầu là D và điểm cuối là I là \(\overrightarrow {DI} \)
Vectơ có điểm đầu là D và điểm cuối là C là \(\overrightarrow {DC} \)
c) Vectơ có điểm đầu là D và bằng vectơ \(\overrightarrow {IB} \) là \(\overrightarrow {DI} \)
Vectơ có điểm đầu là D và bằng vectơ \(\overrightarrow {AB} \) là \(\overrightarrow {DC} \)
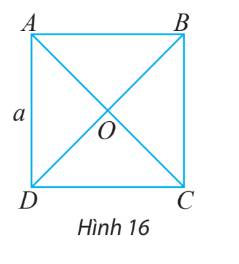


a) \(AC = BD = \sqrt {A{D^2} + D{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow AO = OC = BO = OD = \frac{{a\sqrt 2 }}{2}\)
Suy ra các cặp vectơ bằng nhau và có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\) là:
\(\overrightarrow {AO} \)và \(\overrightarrow {OC} \); \(\overrightarrow {CO} \) và \(\overrightarrow {OA} \); \(\overrightarrow {DO} \) và \(\overrightarrow {OB} \); \(\overrightarrow {OD} \) và \(\overrightarrow {BO} \)
b) Trong hình chỉ có 2 đoạn thẳng AC và BD có độ dài là \(a\sqrt 2\).
Do đó hai vectơ đối nhau và có độ dài bằng \(a\sqrt 2\) là:
\(\overrightarrow {AC} \)và \(\overrightarrow {CA} \); \(\overrightarrow {BD} \) và \(\overrightarrow {DB} \).