Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Ta có
AB=BC và MA=MB; NB=NC => MB=NC
Xét hai tg vuông BMC và tg vuông CNC có
MB=NC (cmt)
BC=CD (cạnh hình vuông)
=> tg BMC= tg CND => ^BMC=^CND (1)
Trong tg vuông BMC có ^BCM+^BMC=90 (2)
Từ (1) và (2) => ^BCM+^CND=90 => ^CHN=90 => MC vuông góc DN
b/
Ta có AB=CD (cạnh hình vuông) và MA=MB; KC=KD => MA=KC
Mà MA//KC
=> AMCK là hình bình hành => AK//MC (3)
Xét tg CDH có ID=IH và KD=KC (đề bài) => IK là đường trung bình => IK//MC (4)
Từ (3) và (4) => AK trùng với IK => A; I; K thẳng hàng
c/
Xét tg ADH có
AI//MC mà MC vuông góc với DN => AI vuông góc với DN => AI là đường cso của tg ADH (5)
Ta có ID=IH (đề bài) => AI là trung tuyến của tg ADH (6)
Từ (5) và (6) => tg ADH cân tại A (tam giác có đường cao đồng thời là đường trung tuyến ... là tam giác cân)

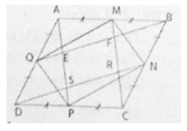
a) Ta có AB // CD (gt)
Suy ra AM // CP (1)
Lại có AM = AB/2; CP = CD/2 (2)
Từ (1) và (2) suy ra AMCP là hình bình hành
Suy ra AP // CM hay ES // FR.
Tương tự ta cũng chứng minh được tứ giác BQDN là hình bình hành nên BQ // DN. Suy ra EF // RS.
Vậy tứ giác EFRS là hình bình hành
b) Đặt PS = x. Suy ra CR = 2x (tính chất đường trung bình)
Từ đó suy ra RF = ES = AE = 2x
Suy ra: ES = 2AP/5 => SEFRS = 2SAMCP/5
Vì SAMCP = SABCD/2 nên SEFRS = SABCD/2
a: Xét tứ giác AMCP có
AM//CP
AM=CP
DO đó: AMCP là hình bình hành
=>AP//MC
b: Gọi giao của AP với DN là G
Xét ΔMBC vuông tại B và ΔNCD vuông tại C có
BC=CD
MB=NC
Do đó: ΔMBC=ΔNCD
=>góc BMC=góc CND
=>góc CND+góc NCM=90 độ
=>CP vuông góc với ND
=>PG vuông góc với DF
Xét ΔDFC có
P là trung điểm của DC
PG//FC
DO đó:G là trung điểm của DF
Xét ΔADF có
AG vừa là đường cao, vừa là trung tuyến
nen ΔADF cân tại A
=>AD=AF