Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 12. Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?
A. Hình chữ nhật. B. Hình thoi. C. Hình bình hành. Câu 13. Cho hình vuông có chu vi 28 cm. Độ dài cạnh hình vuông là: | D. Hình vuông. |
A. 4cm. B. 7cm. C. 14cm. Câu 14. Cho hình vuông có chu vi 32 cm. Độ dài cạnh hình vuông là: | D. 8cm. |
A. 10cm. B. 15cm. C. 5cm. | D. 8cm. |
Câu 12. Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?
A. Hình chữ nhật. B. Hình thoi. C. Hình bình hành. D. Hình vuông.
Câu 13. Cho hình vuông có chu vi 28 cm. Độ dài cạnh hình vuông là:
A. 4cm. B. 7 cm. C. 14cm. D. 8cm.
Câu 14. Cho hình vuông có chu vi 32 cm. Độ dài cạnh hình vuông là:
A. 10cm. B. 15cm. C. 5cm. D. 8 cm

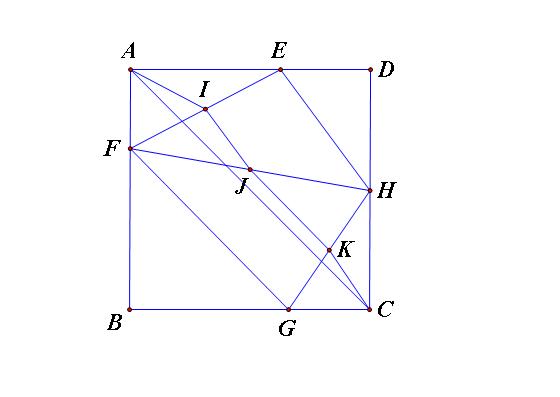
A B C D M E F G H N P Q I K
Gọi EFGH là tứ giác nội tiếp hình vuông
(\(E\in AB,F\in BC,G\in CD,H\in AD\)) , Từ E,F,G,H lần lượt dựng các đường thẳng vuông góc với BD tại P,Q,M,N; I và K là giao điểm của AG và EF.
Ta có : \(AI\ge AM=MP;GI\ge MP=GM;EK\ge EP=BP;KF\ge FQ=BK\)
\(\Rightarrow AG+EF=AI+IG+EK+KF\ge\left(PM+BQ\right)+\left(PN+BP\right)\)
Mặt khác, lại có : \(EH\ge NP;FG\ge MQ\)
\(\Rightarrow EF+FG+GH+HE\ge\left(PM+MQ+BQ\right)+\left(PN+NP+BP\right)\)
\(=BD+BD=2\)
\(\Rightarrow EF+FG+GH+GE\ge2\) (dpcm)
Ta có EF=2.AI,EH=2.IJ,GH=2.CK,EG=2.IK( Áp dụng tính chất đường trung bình và trung tuyến ứng với cạnh huyền trong tam giác vuông)
Suy ra \(P_{EFGH}=2\left(AI+IJ+JK+KC\right)\ge2AC=2\)

a: AE+EB=AB
BF+FC=BC
CG+GD=CD
DH+HA=DA
mà AB=BC=CD=DA và AE=BF=CG=DH
nên EB=FC=GD=HA
Xét ΔEAH vuông tại A và ΔGCF vuông tại C có
EA=GC
AH=CF
Do đó: ΔEAH=ΔGCF
=>EH=GF
Xét ΔEBF vuông tại B và ΔGDH vuông tại D có
EB=GD
BF=DH
Do đó: ΔEBF=ΔGDH
=>EF=GH
Xét ΔEAH vuông tại A và ΔFBE vuông tại B có
EA=FB
AH=BE
Do đó: ΔEAH=ΔFBE
=>EH=EF và \(\widehat{AEH}=\widehat{BFE}\)
\(\widehat{AEH}+\widehat{HEF}+\widehat{BEF}=180^0\)
=>\(\widehat{BFE}+\widehat{BEF}+\widehat{HEF}=180^0\)
=>\(\widehat{HEF}+90^0=180^0\)
=>\(\widehat{HEF}=90^0\)
Xét tứ giác EHGF có
EF=GH
EH=GF
Do đó: EHGF là hình bình hành
Hình bình hành EHGF có EF=EH
nên EHGF là hình thoi
Hình thoi EHGF có \(\widehat{HEF}=90^0\)
nên EHGF là hình vuông
b:
AH+HD=AD
=>AH+1=4
=>AH=3(cm)
ΔAEH vuông tại A
=>\(AE^2+AH^2=EH^2\)
=>\(EH^2=3^2+1^2=10\)
=>\(EH=\sqrt{10}\left(cm\right)\)
EHGF là hình vuông
=>\(S_{EHGF}=EH^2=10\left(cm^2\right)\)

a: Xét ΔABC có
E là trung điểm của AB
F là trung điểm của BC
Do đó: EF là đường trung bình
=>EF//AC và EF=AC/2(1)
Xét ΔCDA có
G là trung điểm của CD
H là trung điểm của DA
Do đó: GH là đường trung bình
=>GH//AC và GH=AC/2(2)
Từ (1) và (2) suy ra EF//GH và EF=GH
hay EFGH là hình bình hành
b: EF=GH=AC/2=3(cm)
FG=EH=BD/2=4(cm)

em gửi bài qua fb thầy chữa cho nhé, tìm fb của thầy bằng sđt: 0975705122 nhé.

mình rất muốn nhưng mình không biết
mình là trần thị lâm hiền ở onlinemath đây mà
Hình tự vẽ nha AN TRAN DOAN.
Bạn lấy E,F,G,H lần lượt là trung điẻm của AB,BC,CD,DA.
Khi đó, EF, FG, GH, HE có độ dài là \(\sqrt{8}\) (cm)
Vậy chu vi của hình thoi bằng:
\(\sqrt{8}\).4= 8. \(\sqrt{2}\) (cm)
Và: AE= 2(cm)