Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A D B C 80độ
Hình 2
1 2 4 3 A 3 4 2 1 B a b
Hình 3
1 2 3 4 87 độ
1. Vì đường thẳng A \(\perp\) với đường thẳng B
\(\Rightarrow\widehat{ABC}=90^o\)
Vì \(\widehat{C}\) và \(\widehat{D}\)là hai góc so le trong
\(\Rightarrow\widehat{C}=\widehat{D}=80^o\)
Vì \(\widehat{C}\)và \(\widehat{BCD}\)kề bù
\(\Rightarrow\widehat{C}+\widehat{BCD}=180^o\)
Mà \(\widehat{C}=80^o\)
\(\Rightarrow80^o+\widehat{BCD}=180^o\)
\(\Rightarrow\widehat{BCD}=180^o-80^o=100^o\)

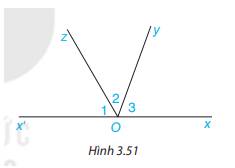
a) Ta có: \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = (\widehat {{O_1}} + \widehat {{O_2}}) + \widehat {{O_3}}\)=\(\widehat {x'Oy} + \widehat {{O_3}}\), mà \(\widehat {x'Oy} + \widehat {{O_3}}\)= 180\(^\circ \) ( 2 góc kề bù)
Vậy \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = 180^\circ \)
b) Vì \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = 180^\circ \)
\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {{O_2}} + 70^\circ = 180^\circ \\ \Rightarrow \widehat {{O_2}} = 180^\circ - 60^\circ - 70^\circ = 50^\circ \end{array}\)
Vậy \(\widehat {{O_2}} = 50^\circ \)

Ta có:
\(\begin{array}{l}a)\widehat {{O_1}} = 135^\circ ;\widehat {{O_3}} = 135^\circ \Rightarrow \widehat {{O_1}} = \widehat {{O_3}}\\b)\widehat {{O_2}} = 45^\circ ;\widehat {{O_4}} = 45^\circ \Rightarrow \widehat {{O_2}} = \widehat {{O_4}}\end{array}\)

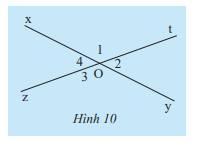
a, các cặp góc đối đỉnh là :
\(\widehat{O_1}\) và \(\widehat{O_3}\)
\(\widehat{O_2}\) và \(\widehat{O_4}\)
b, Ta có : \(\widehat{O_1}+\widehat{O_3}=110^0\)
Mà \(\widehat{O_1}\) đối đỉnh với \(\widehat{O_2}\)
\(\Rightarrow\widehat{O_1}=\widehat{O_3}=\dfrac{110^0}{2}=55^0\)
\(\Rightarrow\widehat{O_1}+\widehat{O_2}=180^0\)
\(\Rightarrow\widehat{O_2}=180^0-55^0=125^0\)
Mà \(\widehat{O_2}\) đối đỉnh với \(\widehat{O_4}\)
\(\Rightarrow\widehat{O_2}=\widehat{O_4}=125^0\)

![]() Biết \widehat{O_1} - \widehat{O_2} = 70^{\circ}O1−O2=70∘
Biết \widehat{O_1} - \widehat{O_2} = 70^{\circ}O1−O2=70∘
Suy ra \widehat{O_1} = \widehat{O_2} + 70^{\circ}O1= O2+70∘
Mà \widehat{O_1}O1 và \widehat{O_2}O2 là hai góc kề bù nên \widehat{O_1} + \widehat{O_2} = 180^{\circ}O1+ O2=180∘.
Thay \widehat{O_1} = \widehat{O_2} + 70^{\circ}O1= O2+70∘ ta được \widehat{O_2} + \widehat{O_2} + 70^{\circ} = 180^{\circ}O2+ O2+70∘=180∘
Hay 2.\widehat{O_2} = 110^{\circ}2.O2=110∘
Suy ra \widehat{O_2} = 55^{\circ}O2=55∘.
Mà hai góc \widehat{O_2}O2 và \widehat{O_4}O4 đối đỉnh nên \widehat{O_4} = 55^{\circ}O4=55∘
![]() Biết \widehat{O_1} + \widehat{O_2} + \widehat{O_3} = 325^{\circ}O1+O2 +O3=325∘.
Biết \widehat{O_1} + \widehat{O_2} + \widehat{O_3} = 325^{\circ}O1+O2 +O3=325∘.
Mà \widehat{O_1}O1 và \widehat{O_2}O2 là hai góc kề bù nên \widehat{O_1} + \widehat{O_2} = 180^{\circ}O1+ O2=180∘.
Suy ra \widehat{O_3} = 325^{\circ} - 180^{\circ} =145^{\circ}O3=325∘−180∘=145∘.
Mà \widehat{O_3}O3 và \widehat{O_4}O4 là hai góc kề bù nên \widehat{O_4} = 180^{\circ} - 145^{\circ} = 35^{\circ}O4=180∘−145∘=35∘.
![]() Biết \widehat{O_1} - \widehat{O_2} = 70^{\circ}O1−O2=70∘
Biết \widehat{O_1} - \widehat{O_2} = 70^{\circ}O1−O2=70∘
Suy ra \widehat{O_1} = \widehat{O_2} + 70^{\circ}O1= O2+70∘
Mà \widehat{O_1}O1 và \widehat{O_2}O2 là hai góc kề bù nên \widehat{O_1} + \widehat{O_2} = 180^{\circ}O1+ O2=180∘.
Thay \widehat{O_1} = \widehat{O_2} + 70^{\circ}O1= O2+70∘ ta được \widehat{O_2} + \widehat{O_2} + 70^{\circ} = 180^{\circ}O2+ O2+70∘=180∘
Hay 2.\widehat{O_2} = 110^{\circ}2.O2=110∘
Suy ra \widehat{O_2} = 55^{\circ}O2=55∘.
Mà hai góc \widehat{O_2}O2 và \widehat{O_4}O4 đối đỉnh nên \widehat{O_4} = 55^{\circ}O4=55∘
![]() Biết \widehat{O_1} + \widehat{O_2} + \widehat{O_3} = 325^{\circ}O1+O2 +O3=325∘.
Biết \widehat{O_1} + \widehat{O_2} + \widehat{O_3} = 325^{\circ}O1+O2 +O3=325∘.
Mà \widehat{O_1}O1 và \widehat{O_2}O2 là hai góc kề bù nên \widehat{O_1} + \widehat{O_2} = 180^{\circ}O1+ O2=180∘.
Suy ra \widehat{O_3} = 325^{\circ} - 180^{\circ} =145^{\circ}O3=325∘−180∘=145∘.
Mà \widehat{O_3}O3 và \widehat{O_4}O4 là hai góc kề bù nên \widehat{O_4} = 180^{\circ} - 145^{\circ} = 35^{\circ}O4=180∘−145∘=35∘.

Hướng dẫn:
Đường tròn đi qua ba dỉnh của tam giác gọi là đường tròn ngoại tiếp tam giác đó. Đẻ vẽ đường tròn ngoại tiếp ta cần xác định tâm của đường tròn đó. Muốn xác định tâm ta vẽ hai đường trung trực và giao điểm hai đường trung trực ( cũng là giao điểm của ba trung trực cần tìm)
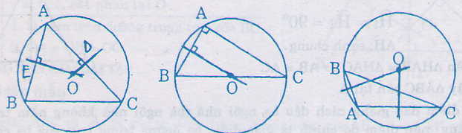
Nhận xét:
- Nếu tam giác có ba góc đều nhọn thì tâm đường tròn ngoại tiếp nằm trong tam giác.
- Nếu tam giác có góc vuông thì tâm đường tròn nằm trên cạnh huyền ( tâm là trung điểm của cạnh huyền)
- Nếu tam giác có góc tù thì tâm đường tròn ngoại tiếp nằm ngoài tam giác
Đường tròn đi qua ba dỉnh của tam giác gọi là đường tròn ngoại tiếp tam giác đó. Đẻ vẽ đường tròn ngoại tiếp ta cần xác định tâm của đường tròn đó. Muốn xác định tâm ta vẽ hai đường trung trực và giao điểm hai đường trung trực ( cũng là giao điểm của ba trung trực cần tìm)

Nhận xét:
- Nếu tam giác có ba góc đều nhọn thì tâm đường tròn ngoại tiếp nằm trong tam giác.
- Nếu tam giác có góc vuông thì tâm đường tròn nằm trên cạnh huyền ( tâm là trung điểm của cạnh huyền)
- Nếu tam giác có góc tù thì tâm đường tròn ngoại tiếp nằm ngoài tam giác

A B C 110*
=> \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\widehat{A}+\widehat{B}=180^o-110^o\)
\(\widehat{A}+\widehat{B}=70^o\)
=> \(\widehat{A}\) = 70o:(3+4).3 = 30o
=> \(\widehat{B}\) = 70o - 30o = 40o
Vậy  = 30o ; \(\widehat{B}\) = 40o và \(\widehat{C}\) = 110o


HÌNH ĐÂU BN
a: góc O1=góc O2=140/2=70 độ
góc O3=góc O4=180-70=110 độ
b: góc O1+góc O3=360/2=180 độ
góc O2+góc O4=180 độ
Góc O1 và O3 là hai góc kề bù rồi nên mặc nhiên tổng của hai góc đó bằng 180 độ nha bạn
Tương tự với cặp góc O2 và O4
=>Không tính được
c: góc O2=góc O1
nên góc O2-góc O1=10 độ là sai đề rồi bạn