KT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 9 2018
Hình nào?
không có hình thì làm làm sao được?
Bạn vẽ hình đi :)
PJ
13 tháng 5 2018
Hình bn tự vẽ nhé!!!!!
a. Ta có :
52 = 25
32 + 42 = 25
=> 52 = 32 + 42 hay BC2 = AB2 + AC2
=> ΔABCΔABC vuông tại A
b.Xét ΔABDΔABD và ΔEBDΔEBD ,có :
BD : cạnh chung
ABDˆ=EBDˆABD^=EBD^ ( BD là tia phân giác của góc B )
BADˆ=BEDˆ=900BAD^=BED^=900
=> ΔABD=ΔEBDΔABD=ΔEBD ( cạnh huyền - góc nhọn )
=> DA = DE
c.Xét ΔADFΔADF và ΔEDCΔEDC ,có :
DA = DE ( c/m b )
FADˆ=DECˆ=900FAD^=DEC^=900
ADFˆ=EDCˆADF^=EDC^ ( 2 góc đối đỉnh )
=> ΔADF=ΔEDCΔADF=ΔEDC ( g.c.g hoặc cạnh góc vuông - góc nhọn kề )
=> DF = DC (1)
mà DC > DE (2) ( trong tam giác vuông cạnh huyền lớn hơn cạnh góc vuông )
Từ (1) và (2) => DF > DE (đpcm )
25 tháng 5 2019
a) Có : \(AB^2+AC^2=3^2+4^2=25\) ; \(BC^2=5^2=25\)
Ta thấy \(AB^2+AC^2=BC^2\Rightarrow\Delta ABC\) vuông tại A
b) Xét \(\Delta ABD\) và \(\Delta EBD\) có:
\(\widehat{BAD}=\widehat{BED}=90^o;BD:chung;\widehat{ABD}=\widehat{EBD}\)
\(\Rightarrow\) \(\Delta ABD\) = \(\Delta EBD\)
\(\Rightarrow\) AD = ED
c) Xét \(\Delta ADF\) và \(\Delta EDC\) có:
\(\widehat{FDA}=\widehat{CDE};AD=ED;\widehat{FAD}=\widehat{CED}=90^o\)
\(\Rightarrow\) \(\Delta ADF\) = \(\Delta EDC\)
\(\Rightarrow\) DF = DC
Xét \(\Delta DEC\) vuông tại E
=> DE < DC mà DC = DF => DE < DF
VM
25 tháng 5 2019
a) Ta có: AB2 + AC2 = 32 + 42 = 9 + 16=25
BC2 = 52 = 25
=> AB2 + AC2 = BC2 (=25)
Áp dụng định lí Py - ta - go đảo
=> ΔABC vuông tại A.
b) Xét 2 Δ vuông ABD và EBD có:
+) ∠BAD = ∠BED = 90 độ
+) Cạnh BD chung
+) ∠B1 = ∠B2 (vì BD là tia phân giác của ∠B)
=> △ABD = ΔEBD (ch - góc nhọn)
=> AD = ED (2 cạnh tương ứng)
c) Xét 2 Δ vuông AFD và ECD có:
+) ∠FAD = ∠CED = 90 độ
+) AD = ED (cmt)
+) ∠FDA = ∠CDE (vì 2 góc đối đỉnh)
=> ΔAFD = ΔECD
=> DF = DC (2 cạnh tương ứng)
Xét △ CED vuông tại E có:
∠CED = 90 độ là góc lớn nhất
=> CD là cạnh lớn nhất
=> CD > ED
mà CD = FD (cmt)
=> FD > ED.
Chúc bạn học tốt!
NQ
0
29 tháng 4 2019
Hình tự vẽ nha
a ) Vì AB = 3 ( gt ) => AB2 = 9
AC = 4 ( gt ) => AC2 = 16
BC = 5 ( gt ) => BC2 = 25
MÀ 25 = 9 + 16
DO đó BC2 = AB2 + AC2
=> \(\Delta\)ABC vuông tại A ( định lí đảo định lí py ta go )
Vậy \(\Delta\)ABC vuông tại A
29 tháng 4 2019
b ) Vì \(\Delta\)ABC vuông tại A ( CM a ) => BAC = 90o hay BAD = 90o
Vì DE \(\perp\)BC ( gt ) => BED = DEC = 90o ( định nghĩa 2 đường thẳng vuông góc )
Vì BD là tia phân giác của góc B ( gt ) => ABD = EBD
Xét \(\Delta\)ABD và \(\Delta\)EBD có :
ABD = EBD ( cmt )
BD chung
BAD = BED ( = 90o )
DO đó \(\Delta\)ABD = \(\Delta\)EBD ( cạnh huyền - góc nhọn )
=> DA = DE ( 2 cạnh tương ứng )
Vậy ..
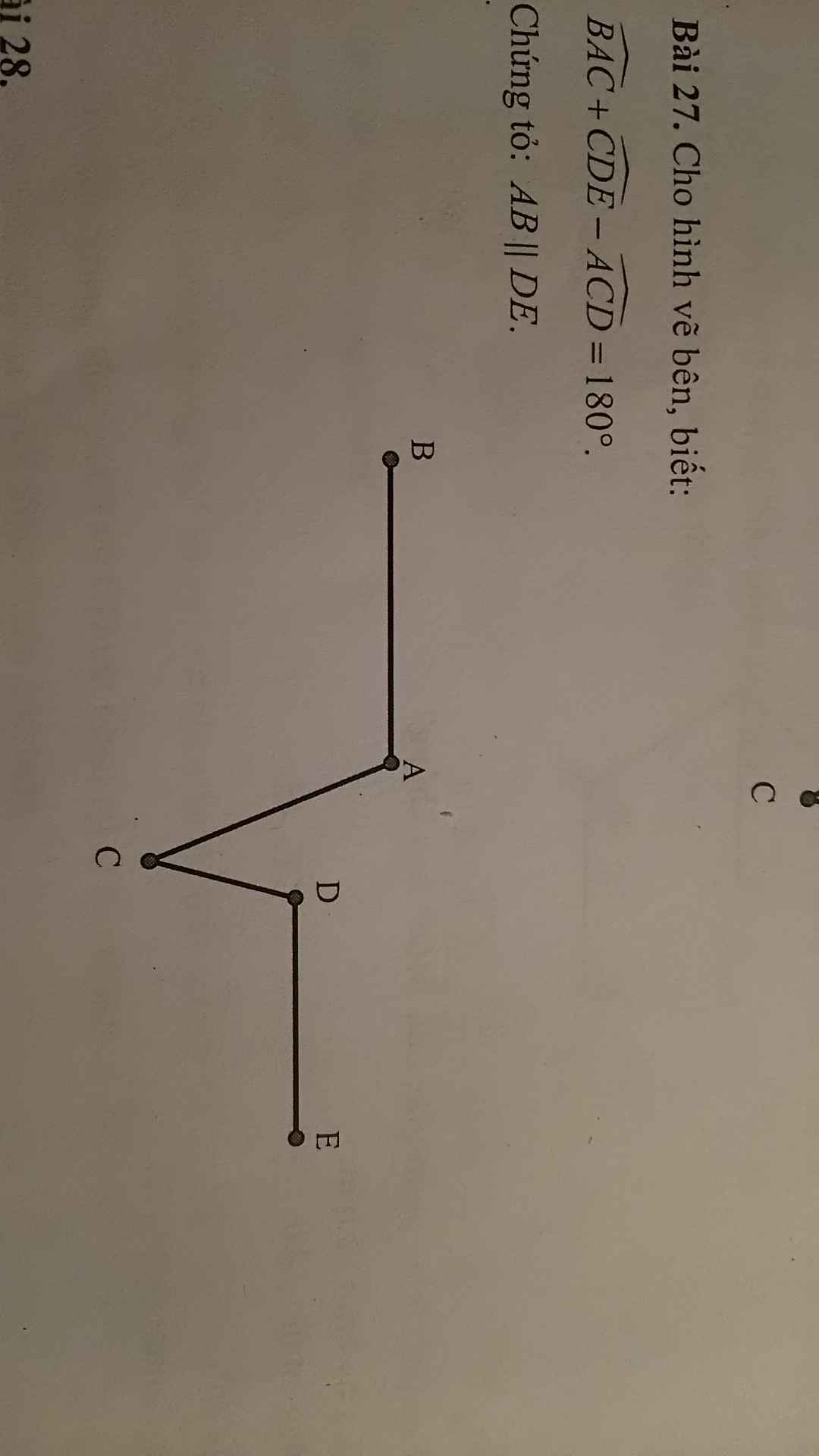
Giải thích các bước giải:Kẻ Cz // AB
⇒ˆABC+ˆBCz=180°⇒ABC^+BCz^=180°(2 góc trrong cùng phía bù nhau)
Ta có: ˆABC+ˆBCD+ˆCDE=360°ABC^+BCD^+CDE^=360°
=ˆABC+ˆBCz+ˆzCD+ˆCDE=360°=ABC^+BCz^+zCD^+CDE^=360°
⇒180°+ˆzCD+ˆCDE=360°⇒180°+zCD^+CDE^=360°
⇒ˆzCD+ˆCDE=360°−180°=180°⇒zCD^+CDE^=360°-180°=180° mà 2 góc này nằm ở vị trí trong cùng phía
=> DE // Cz mà Cz // AB
=> AB // DE (đpcm)