Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có hình vẽ:
A x B C y z 120 160
Vẽ tia Bz nằm trong góc ABC sao cho: Ax // Bz
Do Ax // Cy => Ax // Bz // Cy
Ta có:
- xAB + ABz = 180o (trong cùng phía)
=> 120o + ABz = 180o
=> ABz = 180o - 120o
=> ABz = 60o (1)
- zBC + BCy = 180o (trong cùng phía)
=> zBC + 160o = 180o
=> zBC = 180o - 160o
=> zBC = 20o (2)
Từ (1) và (2), lại có: ABz + zBC = ABC
=> 60o + 20o = ABC
=> ABC = 80o = B
Vậy góc B = 80o
vẽ đường thẳng a đi qua B và a // xA ; a //yC
=> xAB + ABa =180 độ (góc trong cùng phía)
=> ABa = 180 - 120 = 60 độ
aBC + yCB =180 độ (góc trong cùng phía)
=> góc aBC = 180 độ - 160 độ = 20 độ
Vì ABa +aBC = góc B
Thay số ta có :
60độ + 20 độ =80 độ
=> góc B =80 độ (đpcm)

Ta có :
\(\begin{cases}\widehat{BAC}+\widehat{DAC}=180^0\\\widehat{DAC}+\widehat{ACD}+\widehat{ADC}=180^0\end{cases}\)
\(\Rightarrow\widehat{BAC}=\widehat{ACD}+\widehat{ADC}\)
\(\Rightarrow100^0=\widehat{ACD}+\widehat{ADC}\)

a, Ta có:
AB \(\perp\) a
AB \(\perp\) b
\(\Rightarrow\)a // b
b, Ta có: a // b( câu a)
hai góc ADC và DCB là hai góc trong cùng phía
\(\Rightarrow\)DCB = 180\(^0\) - ADC(tính chất hai đường thẳng song song)
\(\Rightarrow\) DCB = 180\(^0\)-120\(^0\) = 60\(^0\)


Từ O vẽ Oz // Mx.
Ta có : Oz // Mx
= > xMO = MOz (so le trong)
Ta lại có : Oz // Mx
Mà Mx // Ny (giả thiết)
=> Oz // Ny (Tiên đề Ơ - clít)
= > zOn + ONy = 180 (Trong cùng phía)
zOn = 180 - ONy = 180 - 110 = 70
Có : MON = MOz + zON = 20 + 70 = 90
=> MO vuông góc với ON

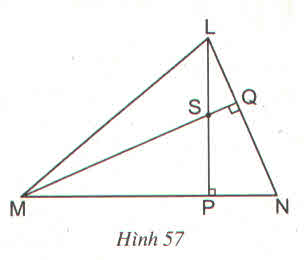
a) Từ hình vẽ ta có: LP ⊥ MN; MQ ⊥ LN
ΔMNL có S là giao điểm của hai đường cao LP và MQ nên S chính là trực tâm của tam giác (định lí ba đường cao).
=> NS cũng là đường cao trong tam giác hay NS ⊥ LM (đpcm).
b) ΔNMQ vuông tại Q có góc LNP = 50o nên góc QMN = 40o
ΔMPS vuông tại P có góc QMP = 40o nên góc MSP = 50o
Vì hai góc MSP và PSQ là hai góc kề bù nên suy ra:
góc PSQ = 180o - 50o = 130o.
Hướng dẫn:
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay
SN ⊥ ML
b) ∆NMQ vuông tại Q có ˆLNPLNP^ =500 nên ˆQMNQMN^ =400
∆MPS vuông tại Q có ˆQMPQMP^ =400 nên ˆMSPMSP^ =500
Suy ra ˆPSQPSQ^ =1300(kề bù)


 -0,75)
-0,75) =21/10
=21/10
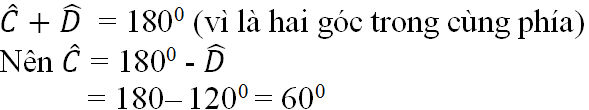

Xét tam giác ABC có \(\widehat{BAC}+\widehat{ACB}+\widehat{B}=180\Rightarrow\widehat{BAD}+\widehat{DAC}+\widehat{ACD}+\widehat{BAD}+\widehat{B}=180\) độ
hay \(20+\widehat{DAC}+25+\widehat{ACD}+50=180\) độ
\(\Rightarrow\widehat{DAC}+\widehat{ACD}=85\) độ
Xét tam giác ADC có \(\widehat{DAC}+\widehat{ACD}+\widehat{ADC}=180\Rightarrow\widehat{ADC}=180-85=95\) độ
Tick hộ nha