K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
15 tháng 6 2018
a) Ta có tAx ^ + xAB ^ = 180 ∘ (hai góc kề bù) mà tAx ^ = 60 ∘
⇒ xAB ^ = 180 ∘ − 60 ∘ = 120 ∘
Mặt khác ABy ^ = 120 ∘
⇒ xAB ^ = ABy ^ mà hai góc này ở vị trí so le trong
⇒ Ax // By
b)
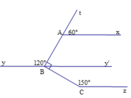
Kẻ tia By' là tia đối của tia By
Ta có: ABy ^ + ABy' ^ = 180 ∘ (hai góc kề bù) mà ABy ^ = 120 ∘
⇒ ABy' ^ = 180 ∘ − 120 ∘ = 60 ∘
Mặt khác ABC ^ = 90 ∘ hay ABy' ^ + y'BC ^ = 90 ∘
⇒ y'BC ^ = 90 ∘ − 60 ∘ = 30 ∘
Ta có y'BC ^ + CBy ^ = 180 ∘ (hai góc kề bù)
⇒ CBy ^ = 180 ∘ − 30 ∘ = 150 ∘
Ta lại có BCz ^ = 150 ∘
⇒ BCz ^ = CBy ^ mà hai góc này ở vị trí so le trong
⇒ By // Cz
PN
1
AH
Akai Haruma
Giáo viên
21 tháng 8 2023
Lời giải:
Ta thấy:
$\widehat{yBA}+\widehat{BAx}=124^0+56^0=180^0$. Mà 2 góc này ở vị trí trong cùng phía nên $By\parallel Ax$ (đpcm)
nha bạn chúc bạn học tốt
CC
0
5 tháng 10 2021
\(a,Ax//By\Rightarrow\widehat{ABy}=\widehat{BAx}=120^0\left(so.le.trong\right)\\ b,\widehat{ABy}=\widehat{BCz}\left(=120^0\right)\)
Mà 2 góc này ở vị trí đồng vị nên \(By//Cz\)
Mà \(By//Ax\) nên \(Cz//Ax\)
Vậy có 3 cặp tia song song là \(Ax//By;By//Cz;Cz//Ax\)
21 tháng 5 2018
Có \(x=by+cz\)
=> \(x\left(1+a\right)=ax+x=ax+by+cz\)
=> \(\frac{1}{1+a}=\frac{x}{ax+by+cz}\)
=> \(\frac{a}{1+a}=\frac{ax}{ax+by+cz}\)
Có \(y=cz+ax\)
=> \(y\left(1+b\right)=by+y=by+cz+ax=ax+by+cz\)
=> \(\frac{1}{1+b}=\frac{y}{ax+by+cz}\)
=> \(\frac{b}{1+b}=\frac{by}{ax+by+cz}\)
Có \(z=ax+by\)
=> \(z\left(1+c\right)=cz+z=cz+ax+by=ax+by+cz\)
=> \(\frac{1}{1+c}=\frac{z}{ax+by+cz}\)
=> \(\frac{c}{1+c}=\frac{cz}{ax+by+cz}\)
=> \(M=\frac{a}{1+a}+\frac{b}{1+b}+\frac{c}{1+c}=\frac{ax}{ax+by+cz}+\frac{by}{ax+by+cz}+\frac{cz}{ax+by+cz}\)
\(=\frac{ax+by+cz}{ax+by+cz}=1\)
Vậy giá trị của M là 1
HN
23 tháng 12 2017
Bài 1:
a) Đồ thị của hàm số y = \(\dfrac{2}{3}\)x là đường thẳng OA với A(3 ; 2)
b) \(2x+\dfrac{3}{4}=\dfrac{-1}{2}\)
\(2x=\dfrac{-1}{2}-\dfrac{3}{4}\)
\(2x=-\dfrac{5}{4}\)
\(x=-\dfrac{5}{4} :2\)
\(x=-\dfrac{5}{8}\)
c) Ta có: x.2 = y.4 \(\Rightarrow\dfrac{x}{4}=\dfrac{y}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\dfrac{x}{4}=\dfrac{y}{2}=\dfrac{x-y}{4-2}=\dfrac{12}{2}=6\)
\(\Rightarrow\left\{{}\begin{matrix}x=6.4=24\\y=6.2=12\end{matrix}\right.\)
Vậy x = 24; y = 12.
HN
23 tháng 12 2017
Bài 2:
A P x y Q B M
a) NB?
Vì M là trung điểm của AB
nên MA = MB = \(\dfrac{AB}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Ta có: \(\left\{{}\begin{matrix}Ax\perp AB\\By\perp AB\end{matrix}\right.\)
\(\Rightarrow Ax//By\)
b) Xét hai tam giác vuông AMP và BMQ có:
MA = MB (gt)
\(\widehat{AMP}=\widehat{BMQ}\) (đối đỉnh)
\(\Rightarrow\Delta AMP=\Delta BMQ\left(cgv-gn\right)\)
\(\Rightarrow\) MP = MQ
Xét hai tam giác AMQ và BMP có:
MA = MB (gt)
\(\widehat{AMQ}=\widehat{BMP}\) (đối đỉnh)
MQ = MP (cmt)
\(\Rightarrow\Delta AMQ=\Delta BMP\left(c-g-c\right)\)
\(\Rightarrow\widehat{AQM}=\widehat{BPM}\)
Mà hai góc này ở vị trí so le trong
\(\Rightarrow\) AQ // BP (đpcm).
23 tháng 12 2017
1)
a)
_ Xác định điểm A(3;2)
_ Đường thẳng OA là đồ thị của hàm số \(y=\dfrac{2}{3}x\)
y x O y=2/3x A
24 tháng 12 2017
a)Hàm số y=\(\dfrac{2}{3}\)x
Đi qua x=0 \(\rightarrow\)y=0 0(0:0)
x=3\(\rightarrow\)y=2 A(3:2)
KV
30 tháng 8 2023
a) Vẽ tia By' là tia đối của tia By
Ta có:
∠ABy' + ∠ABy = 180⁰ (kề bù)
⇒ ∠ABy' = 180⁰ - ∠ABy
= 180⁰ - 135⁰
= 45⁰
⇒ ∠ABy' = ∠BAx = 45⁰
Mà ∠ABy' và ∠BAx là hai góc so le trong
⇒ By // Ax
b) Ta có:
∠CBy' = ∠ABC - ∠ABy'
= 75⁰ - 45⁰
= 30⁰
⇒ ∠CBy' = ∠BCz = 30⁰
Mà ∠CBy' và ∠BCz là hai góc so le trong
⇒ By // Cz