Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

V ( C ; 2 ) ( I G H F ) = ( A I F D ) ; Đ I ( A I F D ) = C I E B .
Đáp án C.

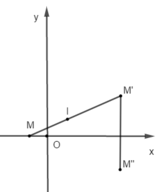
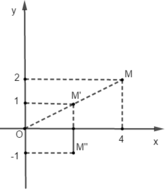
V ( 0 ; 1 / 2 ) ( M ( 4 ; 2 ) ) = M ' ( 2 ; 1 ) ; Đ O x ( M ' ( 2 ; 1 ) ) = M " ( 2 ; - 1 ) .
Đáp án A.

Đáp án C
Những phát biểuđúng: 1; 4; 5; 6; 7; 8; 9; 10; 11; 13; 14
2. Qua phép vị tự có tỉ số , đường tròn có tâm là tâm vị tự sẽ biến thành 1 đường tròn đồng tâm với đường tròn ban đầu và có bán kính = k. bán kính đường tròn ban đầu.
3. Qua phép vị tự có tỉ số đường tròn biến thành chính nó.
12. Phép vị tự với tỉ số k = biến tứ giác thành tứ giác bằng nó

V V ( I ; - 2 ) ( M ( - 1 ; 0 ) ) = M ' ( 8 ; 3 ) ; Đ O x ( M ' ) = M " ( 8 ; - 3 )
Đáp án A

Phương trình đường thẳng d: x - y - 1= 0
Lấy M(x; y) thuộc d
Phép vị tự tâm O(0; 0) tỉ số k = 3 biến điểm M thành M’(x’; y’) thì O M ' → = 3 O M → ⇔ x ' = 3 x y ' = 3 y ⇔ x = 1 3 x ' y = 1 3 y '
Phép đối xứng trục Ox biến M’(x’; y’) thành M’’(x’’; y’’)
Thay vào phương trình d ta được: ⇔ x ' ' = x ' y ' ' = − y ' ⇔ x = 1 3 x ' ' y = − 1 3 y ' '
Hay x’’ + y’’ - 3 = 0
Vậy phương trình đường thẳng d’: x + y - 3 = 0.
Đáp án B

Gọi tam giác A'B'C' là ảnh của tam giác ABC qua phép biến hình trên.

(e)Phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng qua trục Oy và phép vị tự tâm O tỉ số k = -2
+) Qua phép đối xứng qua trục Oy biến tam giác ABC thành tam giác A 1 B 1 C 1
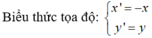
Do đó, tọa độ A 1 - 1 ; 1 ; B 1 0 ; 3 v à C 1 - 2 ; 4 .
+) Qua phép vị tự tâm O tỉ số k = -2 biến tam giác A 1 B 1 C 1 thành tam giác A 2 B 2 C 2
Biểu thức tọa độ :
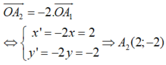
Tương tự; B 2 0 ; - 6 v à C 2 4 ; - 8
Vậy qua phép đối xứng trục Oy và phép vị tự tâm O tỉ số k = -2, biến các điểm A, B, C lần lượt thành
A 2 2 ; - 2 ; B 2 0 ; - 6 v à C 2 4 ; - 8 .

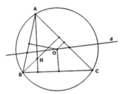
Phép đối xứng qua đường thẳng ***** biến tam giác AEO thành tam giác BFO, phép vị tự tâm B, tỉ số 2 biến tam giác BFO thành tam giác BCD. Do đó ảnh của tam giác AEO qua phép đồng dạng đã cho là tam giác BCD.
Phép đối xứng qua đường thẳng biến tam giác AEO thành tam giác BFO, phép vị tự tâm B, tỉ số 2 biến tam giác BFO thành tam giác BCD. Do đó ảnh của tam giác AEO qua phép đồng dạng đã cho là tam giác BCD.

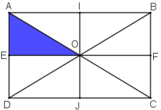
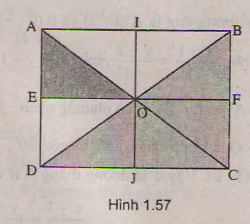
+ Lấy đối xứng qua đường thẳng IJ.
IJ là đường trung trực của AB và EF
⇒ ĐIJ(A) = B; ĐIJ (E) = F
O ∈ IJ ⇒ ĐIJ (O) = O
⇒ ĐIJ (ΔAEO) = ΔBFO
+ ΔBFO qua phép vị tự tâm B tỉ số 2
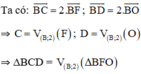
Vậy ảnh của ΔAEO qua phép đồng dạng theo đề bài là ΔBCD.
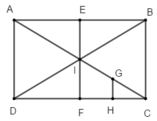
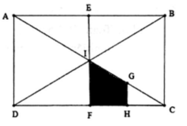
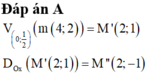
Đáp án A:
Đ O Δ O C F = Δ O A E V A ; 2 Δ O A E = Δ C A B
Đáp án B:
Đ A C Δ O C F = Δ O C M V C ; 2 Δ O C M = Δ A C B
Đáp án C:
V C ; 2 Δ O C F = Δ A C D Đ O Δ A C D = Δ C A B
Đáp án D:
Đ B D Δ O C F = Δ O A N V O ; − 1 Δ O A N = Δ O C M
Vậy phép đồng dạng P được hợp thành bởi phép đối xứng trục BD và phép vị tự tâm O, tỉ số k = -1 không biến tam giác OCF thành tam giác CAB.
Đáp án D