Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có È là đường trung bình của hình thang ABCD.
Þ EF//AB.
Suy ra EF ^ AD
Khi đó EF vừa trung tuyến, vừa là đường cao của tam giác AFD Þ ĐPCM.
b) Tam giác AFD cân tại F nên E A F ^ = E D F ^
Suy ra F A B ^ = C D F ^
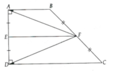

A B C D . E F Giải E là trung điểm AC F là trung điểm BD => EF // CD // AB => góc AEF vuông góc CEF vuông Xét tam giác AEF và CEF có : /\ AEF = /\ CEF = 90 độ EF chung AE = AC (gt) => tam giác AEF = CEF ( cạnh góc cạnh ) => FA = FC => tam giác AFC cân tại F ( đpcm )

Giải
Vì E là trung điểm AC
F là trung điểm BD
=> EF // CD // AB
=>góc AEF \(\perp\) CEF vuông
Xét \(\Delta\) AEF và CEF có
:/\ AEF = /\ CEF = 90 độ
EF chung
AE = AC (gt)
=> \(\Delta\) AEF = CEF ( cạnh góc cạnh )
=>\(\Delta\) AFD là tam giác cân
b, Vì \(\Delta\)AFD là \(\Delta\)cân nên
\(\Rightarrow\)Góc FAD = góc FDA
Ta có : góc A = góc BAF + góc FAD
Góc D = góc CDF + góc FDA
mà góc A = góc D = 90 độ
=> góc BAF = góc CDF

a: Hình thang ABCD có
E là trung điểm của AD
F là trung điểm của BC
Do đó: EF là đường trung bình của hình thang ABCD
Suy ra: EF//AB//CD
mà AB\(\perp\)AD
nên EF\(\perp\)AD
Xét ΔFAD có
FE là đường cao ứng với cạnh AD
FE là đường trung tuyến ứng với cạnh AD
Do đó: ΔFAD cân tại F
b) Ta có: \(\widehat{BAF}+\widehat{DAF}=90^0\)
\(\widehat{CDF}+\widehat{FDA}=90^0\)
mà \(\widehat{FAD}=\widehat{FDA}\)(ΔFAD cân tại F)
nên \(\widehat{BAF}=\widehat{CDF}\)
a: Hình thang ABCD có
E là trung điểm của AD
F là trung điểm của BC
Do đó: EF là đường trung bình của hình thang ABCD
Suy ra: EF//AB//CD
mà AB\(\perp\)AD
nên EF\(\perp\)AD
Xét ΔFAD có
FE là đường cao ứng với cạnh AD
FE là đường trung tuyến ứng với cạnh AD
Do đó: ΔFAD cân tại F
b) Ta có: \(\widehat{BAF}+\widehat{DAF}=90^0\)
\(\widehat{CDF}+\widehat{FDA}=90^0\)
mà \(\widehat{FAD}=\widehat{FDA}\)(ΔFAD cân tại F)
nên \(\widehat{BAF}=\widehat{CDF}\)

a: Xét ΔIBE có
IA vừa là đường cao, vừa là đường trung tuyến
nên ΔIBE cân tại I
=>IA là phân giác của góc BIE
=>góc EIA=góc BIA
=>góc BIA=góc DIC
b: Xét ΔIBE và ΔIFC có
góc IBE=góc IFC
góc BIE=góc FIC
Do đó: ΔIBE=ΔIFC
Suy ra: IB/IF=IE/IC
mà IB=IE
nên IF=IC
=>ΔIFC cân tại I
mà ID là đường cao
nên D là trung điểm của CF
=>AD là đường trung trực của CF

A B C D E F
a, Vì E là trung điểm của AD => AE=ED=> EF là đường trung tuyến của tam giác AFD (1 )
Ta có : E là trung điểm AD, F là trung điểm BC => EF là đường trung bình của hình thang ABCD
=> EF//AB//DC
Vì EF//AB, AD_|_ AB => EF_|_AD=> EF là đường cao của tam giác AFD (2)
Ta có : AE=ED, EF_|_ AD => EF là đường trung trực của tam giác AFD (3)
Từ ( 1 ), (2), (3) => tam giác AFD cân tại F
b, Vì tam giác AFD cân tại F => \(\widehat{FAD}=\widehat{FDA}\)
Ta có : \(\widehat{A}=\widehat{BAF}+\widehat{FAD}\)
\(\widehat{D}=\widehat{CDF}+\widehat{FDA}\)
mà \(\widehat{A}=\widehat{D}=90^0\)
=> \(\widehat{BAF}=\widehat{CDF}\)

a) FN là đường trung bình của tam giác ADC
\(\Rightarrow FN=\frac{AD}{2}\)
EM là đường trung bình của tam giác ADB
\(\Rightarrow EM=\frac{AD}{2}\)
NE là đường trung bình của tam giác ABC
\(\Rightarrow EN=\frac{CB}{2}\)
FM là đường trung bình của tam giác BDC
\(\Rightarrow FM=\frac{CB}{2}\)
Mà AD = BC (gt)
\(\Rightarrow FN=EM=EN=FM=\frac{AD}{2}=\frac{CB}{2}\)
\(\Rightarrow FN=EM=EN=FM\)
=> Tứ giác FNEM là hình thoi
b) FM là đường trung bình của tam giác BDC
\(\Rightarrow FM//BC\Leftrightarrow\widehat{DFM}=\widehat{DCB}=80^o\)
FN là đường trung bình của tam giác ADC
\(\Rightarrow FN//AD\Leftrightarrow\widehat{CFN}=\widehat{CDA}=40^o\)
Ta có \(\widehat{CFN}+\widehat{MFN}+\widehat{DFM}=180^o\)
\(\Leftrightarrow40^o+\widehat{MFN}+80^o=180^o\Leftrightarrow\widehat{MFN}=60^o\)

B A M E F D C 1 60 độ
a) - Vì ABCD là hình bình hành(gt)
\(\Rightarrow BC
//AD\)và BC=AD
Mà \(E\in BC,F\in AD\)và \(BE=\frac{1}{2}BC,\text{AF}=\frac{1}{2}AD\)(gt)
Nên\(BE//\text{AF}\)và BE=AF
=> ABEF là hình bình hành (1)
Mặt khác AD=2AB(gt)
=>\(AB=\frac{AD}{2}\)
\(\text{AF}=\frac{AD}{2}\left(gt\right)\)
Nên AB=AF(2)
Từ (1) và (2) => ABEF là hình thoi
=> \(AE\perp BF\)
b) Ta có BC//FD(BC//AD,F thuộc AD)
=> BCDF là hình thang (3)
- Vì ABCD là hình bình hành(gt)
Nên \(\widehat{BAD}=\widehat{C}=60^o\)(4)
- Ta có : \(\widehat{B\text{AF}}+\widehat{ABE}=180^0\)(Trong cùng phía,BC//AD)
\(\widehat{ABE}=180^0-\widehat{B\text{AF}}\)
\(\widehat{ABE}=180^o-60^o=120^o\)
Mà ABEF là hình thoi
=> \(\widehat{B_1}=\widehat{\widehat{\frac{ABE}{2}}=\frac{120^o}{2}=60^o}\)(5)
Từ (4) và (5) => \(\widehat{C}=\widehat{B_1}\)(6)
Từ (3) và (6)
=> BCDF là hình thang cân
c) Vì ABCD là hình bình hành(gt)
Nên AB//CD và AB=CD
Mà M thuộc AB và AB=BM(M đối xứng với A qua B)
=> B là trung điểm của AB
Nên BM//CD và BM=CD
=> BMCD là hình bình hành (7)
- Xét \(\Delta ABF\)có ;
AB=AF(cmt)
=> \(\Delta ABF\)cân tại A
Mà \(\widehat{B\text{AF}}=60^o\)(gt)
Nên \(\Delta ABF\)đều
=> AB=BF=AF
- Xét \(\Delta ABD\)có:
BF là đường trung tuyến ứng với AD (FA=FD)
\(BF=\frac{1}{2}AD\)(BF=FA mà \(FA=\frac{1}{2}AD\))
Nên \(\Delta ABD\)vuông tại B
=> \(\widehat{MBD}=90^0\)(8)
Từ (7) và (8) =>BMCD là hình chữ nhật
Mà E là trung điểm của BC(gt)
Nên E là trung điểm của MD
Hay E,M,D thẳng hàng
Câu hỏi của Yaden Yuki - Toán lớp 8 - Học toán với OnlineMath Em tham khảo bài làm ở link này nhé!
Hình thang ABCD có
E là trung điểm của AD
F là trung điểm của BC
Do đó: EF là đường trung bình của hình thang ABCD
Suy ra: EF//AB//CD
mà AB\(\perp\)AD
nên EF\(\perp\)AD
Xét ΔFAD có
FE là đường cao ứng với cạnh AD
FE là đường trung tuyến ứng với cạnh AD
Do đó: ΔFAD cân tại F
b) Ta có: \(\widehat{BAF}+\widehat{DAF}=90^0\)
\(\widehat{CDF}+\widehat{FDA}=90^0\)
mà \(\widehat{FAD}=\widehat{FDA}\)(ΔFAD cân tại F)
nên \(\widehat{BAF}=\widehat{CDF}\)