Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có hình thang vuông ABCD, nên ta có: AB^2 + BC^2 = AC^2 AD^2 + DC^2 = AC^2
Vì AB = 15cm, AD = 20cm và ABCD là hình thang vuông, nên ta có: 15^2 + BC^2 = AC^2 20^2 + DC^2 = AC^2
Vì 2 đường chéo AC và BD vuông góc tại O, nên ta có: OB^2 + BC^2 = OC^2 OD^2 + DC^2 = OC^2
Vì ABCD là hình thang vuông, nên ta có: OB^2 + BC^2 = OD^2 + DC^2
Từ hai phương trình trên, ta có thể suy ra OB = OD.
b) Ta có thể tính đường chéo AC bằng cách sử dụng định lí Pythagoras trên tam giác vuông AOC: AC^2 = AO^2 + OC^2
Vì OB = OD, nên ta có AO = OD = OB.
Vậy, ta có: AC^2 = OB^2 + OC^2
c) Để tính diện tích SABCD, ta có thể sử dụng công thức
a: ΔABD vuông tại A
=>BD^2=AB^2+AD^2=625
=>BD=25cm
ΔABD vuông tại A có AO là đường cao
nên BO*BD=BA^2 và DO*DB=DA^2 và AO^2=OD*OB
=>BO=15^2/25=9cm; DO=20^2/25=16cm; AO^2=9*16=144
=>AO=12cm
b: Xét ΔOAB vuông tại O và ΔOCD vuông tại O có
góc OAB=góc OCD
=>ΔOAB đồng dạng với ΔOCD
=>OA/OC=OB/OD
=>9/16=12/OC
=>OC=16*12/9=16*4/3=64/3cm
AC=12+64/3=100/3cm
c: \(S_{ABCD}=\dfrac{1}{2}\cdot AC\cdot BD=\dfrac{1}{2}\cdot\dfrac{100}{3}\cdot25=\dfrac{50}{3}\cdot25=\dfrac{1250}{3}\left(cm^2\right)\)

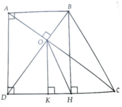
a, Tính được DB=15cm. A D B ^ ≈ 37 0 ; A B D ^ ≈ 53 0
b, Tính được AO=7,2cm, DO=9,6cm và AC=20cm
c, Kẻ OK ⊥ DC tại K
DH=AB=9cm, DC=16cm, DK=5,76cm và OK=7,68cm
Từ đó S D O H = O K . D H 2 = 7 , 68 . 9 2 = 34,56 c m 2

Do góc <DAB = <CBD =90 độ và <ABD = < BDC (do AB//CD)
-> Tam giác ADB và BCD đồng dạng
=> AD/BC = DB/CD <-> AD.CD=BC.DB <-> BC.DB = 12.25 =300 (1)
Mặt khác do tam giác DBC vuông tại B nên theo định lý Pitago :
BD^2+BC^2=CD^2
hay BC^2+BD^2 =625 (2)
Từ (1) và (2) ta giải hệ thì có BC, BD:
BD^2+ (300/BD)^2=625 -> BD^4 - 625 BD^2 +900 = 0 -> BD^2 = (625+can( 387025))/2 ( loại nghiệm còn lại do BD là cạnh huyền của tam giác vuông ABD nên BD^2 > AD^2 =144)
-> BD = can( (625+can( 387025))/2 )
-> BC = 3000/BD
Do góc <DAB = <CBD =90 độ và <ABD = < BDC (do AB//CD)
-> Tam giác ADB và BCD đồng dạng
=> AD/BC = DB/CD <-> AD.CD=BC.DB <-> BC.DB = 12.25 =300 (1)
Mặt khác do tam giác DBC vuông tại B nên theo định lý Pitago :
BD^2+BC^2=CD^2
hay BC^2+BD^2 =625 (2)
Từ (1) và (2) ta giải hệ thì có BC, BD:
BD^2+ (300/BD)^2=625 -> BD^4 - 625 BD^2 +900 = 0 -> BD^2 = (625+can( 387025))/2 ( loại nghiệm còn lại do BD là cạnh huyền của tam giác vuông ABD nên BD^2 > AD^2 =144)
-> BD = can( (625+can( 387025))/2 )
-> BC = 3000/BD
~~~~~~~~~~~ai đi ngang qua nhớ để lại k ~~~~~~~~~~~~~
~~~~~~~~~~~~ Chúc bạn sớm kiếm được nhiều điểm hỏi đáp ~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~ Và chúc các bạn trả lời câu hỏi này kiếm được nhiều k hơn ~~~~~~~~~~~~

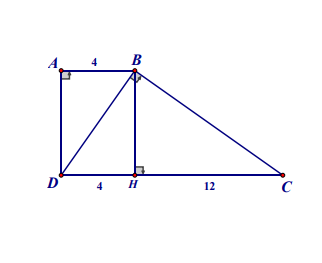
Áp dụng HTL:
\(BH^2=DH\cdot HC=48\Leftrightarrow BH=4\sqrt{3}\left(cm\right)\)
Dễ thấy ABHD là hcn nên \(BH=AD=4\sqrt{3}\left(cm\right)\)
Ta có:
\(\tan\widehat{ABD}=\dfrac{AD}{AB}=\dfrac{4\sqrt{3}}{4}=\sqrt{3}=\tan60^0\\ \Leftrightarrow\widehat{ABD}=60^0\\ \Leftrightarrow\widehat{ABC}=\widehat{ABD}+\widehat{CBD}=60^0+90^0=150^0\)
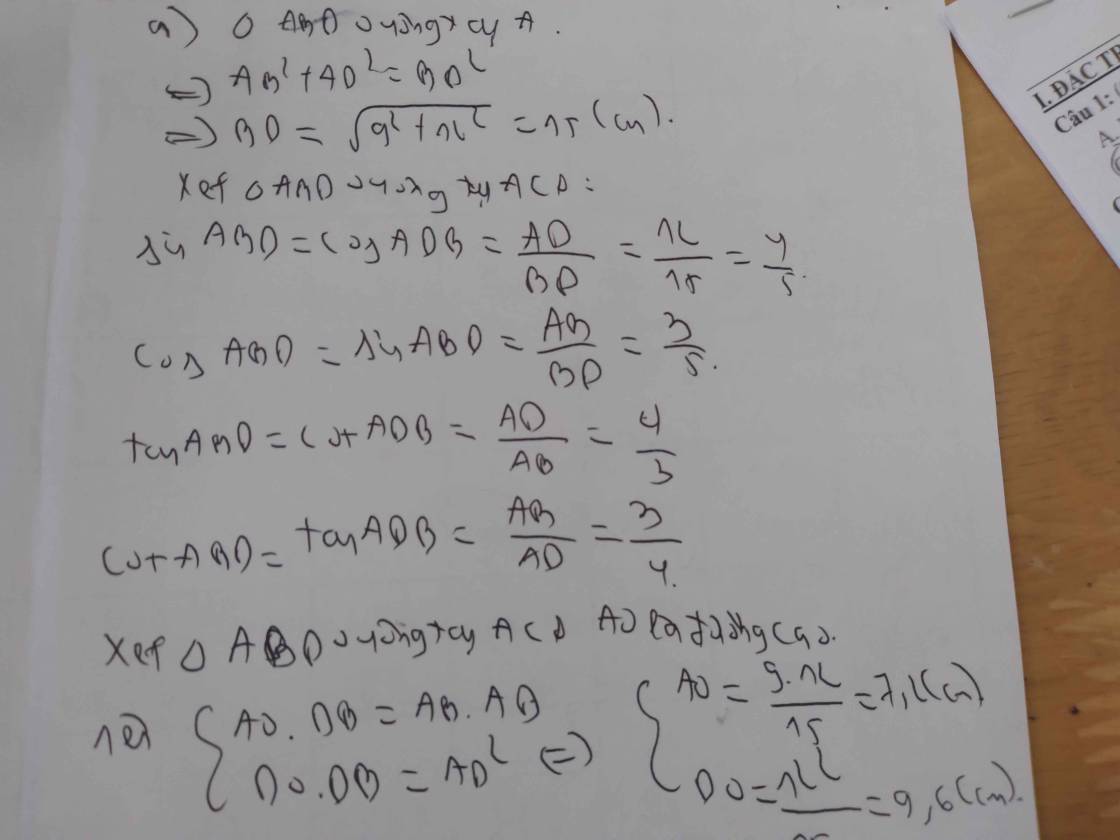


mình mới từ lớp 8 -> 9 nên chắc không thể làm bài này
bn có thể tham khảo nếu đúng k cho mk nhé
ok
hình vẽ
từ B kẻ dừng thẳng vuông góc với Cd tại e
ta có
BE = Ad = 12 cm
áp dụng ding lý py-ta-go trong tam giác BCE
tính được Bc
còn lại thì mình chưa học lượng giác nên chịu thôi
hình vẽ
cảm ơn bạn ạ :v mình ghi nhầm số nên tính không ra