Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lấy K là trung điểm của CD , I là trung điểm của DN
Chứng minh tứ giác ABKD là hình vuông
=> ˆADB=45o(1)ADB^=45o(1)
Chứng minh △ DBC△ DBC là tam giác vuông cân =>ˆDBC=90o(2)=>DBC^=90o(2)
Từ (1) và (2) ta được ˆABC=135oABC^=135o
Ta có △ DBN△ DBN vuông tại B có BI là trung tuyến nên BI =DI =IN (3)
lại có △ DMN△ DMN vuông tại M có MI là trung tuyến nên MI= DI =IN(4)
Kết hợp (3)(4) ta có +△ MIB+△ MIB cân tại I nên ˆIMB=ˆIBMIMB^=IBM^(5)
+△ OIN+△ OINcân tại I nên ˆIBN=ˆBNI(6)IBN^=BNI^(6)
Từ (5) (6) ta được : ˆIBM+ˆIBN+ˆIMB+ˆBNI=270oIBM^+IBN^+IMB^+BNI^=270o
=>ˆMIN=360o−270o=90o=>MIN^=360o−270o=90o
=>MI⊥ DN=>MI⊥ DN
Tam giác vuông DMN có MI vừa là tt vừa là đường cao nên là tam giác vuông cân
thay đổi thông tin đi


Đáp án cần chọn là: D
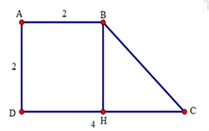
Từ B kẻ BH vuông góc với CD.
Tứ giác ABHD là hình thang có hai cạnh bên AD // BH nên AD = BH, AB = DH.
Mặt khác, AB = AD = 2cm nên suy ra BH = DH = 2cm.
Do đó: HC = DC – HD = 4 – 2 = 2cm.
Tam giác BHC có BH = HC = 2cm nên tam giác BHC cân đỉnh H.
Lại có B H C ^ = 90 ° (do BH ⊥ CD) nên tam giác BHC vuông cân tại H.
Do đó B C H ^ = 180 ° - B H C ^ ÷ 2 = 180 ° - 90 ° ÷ 2 = 45 °
Xét hình thang ABCD có:
A B C ^ = 360 ° - A ^ + D ^ + C ^ = 360 ° - 90 ° + 90 ° + 45 ° = 135 °
Vậy A B C ^ = 135 ° .

Kẻ BH ⊥ CD
Ta có: AD ⊥ CD ( Vì ABCD là hình thang vuông có ∠ A = ∠ D = 90 0 )
Suy ra: BH // AD
Hình thang ABHD có hai cạnh bên song song nên HD = AB và BH = AD
AB = AD = 2cm (gt)
⇒ BH = HD = 2cm
CH = CD – HD = 4 – 2 = 2 (cm)
Suy ra: ∆ BHC vuông cân tại H
Hình đây ạ !!:



Lấy K là trung điểm của CD , I là trung điểm của DN
Chứng minh tứ giác ABKD là hình vuông
=> ˆADB=45o(1)ADB^=45o(1)
Chứng minh △ DBC△ DBC là tam giác vuông cân =>ˆDBC=90o(2)=>DBC^=90o(2)
Từ (1) và (2) ta được ˆABC=135oABC^=135o
Ta có △ DBN△ DBN vuông tại B có BI là trung tuyến nên BI =DI =IN (3)
lại có △ DMN△ DMN vuông tại M có MI là trung tuyến nên MI= DI =IN(4)
Kết hợp (3)(4) ta có +△ MIB+△ MIB cân tại I nên ˆIMB=ˆIBMIMB^=IBM^(5)
+△ OIN+△ OINcân tại I nên ˆIBN=ˆBNI(6)IBN^=BNI^(6)
Từ (5) (6) ta được : ˆIBM+ˆIBN+ˆIMB+ˆBNI=270oIBM^+IBN^+IMB^+BNI^=270o
=>ˆMIN=360o−270o=90o=>MIN^=360o−270o=90o
=>MI⊥ DN=>MI⊥ DN
Tam giác vuông DMN có MI vừa là tt vừa là đường cao nên là tam giác vuông cân