Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
O A B D C E
+) Tứ giác ABCD kà hình thang cân => góc ADC = BCD và AD = BC
=> tam giác ODC cân tại O => OD = OC
mà AD = BC => OA = OB
+) tam giác ODB và OCA có: OD = OC; góc DOC chung ; OB = OA
=> Tam giác ODB = OCA (c - g - c)
=> góc ODB = OCA mà góc ODC = OCD => góc ODC - ODB = OCD - OCA
=> góc EDC = ECD => tam giác EDC cân tại E => ED = EC (2)
Từ (1)(2) => OE là đường trung trực của CD
=> OE vuông góc CD mà CD // AB => OE vuông góc với AB
Tam giác OAB cân tại O có OE là đường cao nên đồng thời là đường trung trực
vậy OE là đường trung trực của AB

Xét ΔQDC có AB//DC
nên QA/AD=QB/BC
mà AD=BC
nên QA=QB
QA+AD=QD
QB+BC=QC
mà QA=QB và AD=BC
nên QD=QC
Xét ΔABD và ΔBAC có
AB chung
BD=AC
AD=BC
=>ΔABD=ΔBAC
=>góc DBA=góc BAC
=>góc PAB=góc PBA
=>PA=PB
PA+PC=AC
PB+PD=BD
mà PA=PB và AC=BD
nên PC=PD
PA=PB
QA=QB
=>PQ là trung trực của AB
PD=PC
QD=QC
=>PQ là trung trực của DC

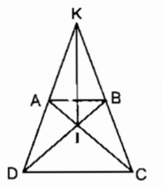
∆ ACD = ∆ BDC (c.c.c)
Suy ra 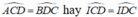
⇒ Tam giác ICD cân tại I.
do đó ID = IC (1)
Tam giác KCD có hai góc ở đáy bằng nhau ∠ C = ∠ D nên tam giác KCD cân tại K
⇒ KD = KC (2)
Từ (1) và (2) suy ra KI là đường trung trực của CD.
Chứng minh tương tự có IA = IB, KA = KB
Suy ra KI là đường trung trực của AB

Gọi H là trung điểm DC.
Chứng minh HE// IF( vì cùng //BC)
=> HE vuông FK ( vì FK vuông IF)
Tương tự HF// EI( vì cùng //AD)
=> HF vuông EK( vì EK vuông IE)
Xét tam giác EFH có EK và FK là 2 đường cao nên K là trực tâm. Suy ra HK vuông FE mà FE //DC nên HK vuông DC tại H suy ra tam giác KDC cân tại K. Nên KD=KC
