Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
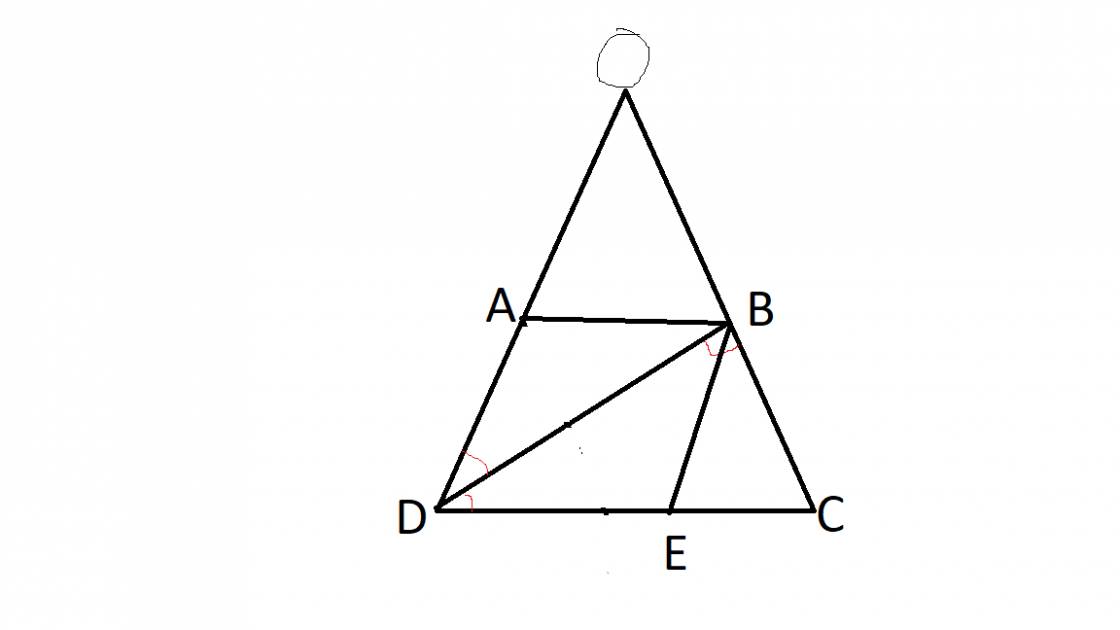
Ta có: AD=BC=3cm (t/c hthang)
Vì AB//CD(gt) nên \(\widehat{ABD}=\widehat{BDC}\left(SLT\right)\)
Mà \(\widehat{ADC}=\widehat{BDC}\) (do BD là tia pgiac góc D)
=>∠ABD=∠BDC
=>∆ABD cân tại A
=>AD=BC=3cm
Vì ∆DBC vuông tại B
nên ∠BDC+∠C=90o
Mà ∠ADC=∠C (do ABCD là hình thang cân)
và ∠BDC=1/2 ∠ADC
=> ∠BCD=1/2∠C
Khi đó: ∠C+1/2∠C=90o=>∠C=60o
- Kẻ từ B 1 đường thẳng // AD cắt CD tại E
Hình thang ABED có hai cạnh bên song song nên AB = DE và AD = BE
⇒ DE = 3 (cm), BE = 3 (cm)
Mà ∠BEC=∠ADC(đồng vị)
=>∠BEC=∠C
=>∆BEC cân tại B có ∠C=60o
=>∆BEC là ∆ cả cân cả đều
=> EC=BC=3cm
Ta có: CD = CE + ED = 3 + 3 = 6(cm)
Chu vi hình thang ABCD bằng:
AB + BC + CD + DA = 3 + 3 + 6 + 3 = 15 (cm)
Bài 2:
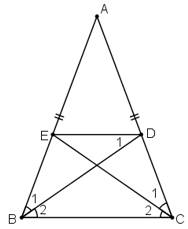
Ta có: ∆ABC là ∆ cân tại A(gt)
=>∠ABC=∠ACB
+Ta có BD là tia pgiac của ∠ABC
=>∠B1=∠B2=1/2∠ABC
+Ta có CE là tia pgiac ∠ACB
=>C1=C2=1/2∠ACB
Xét ∆
AEC và ΔADB có:
+∠A chung
+AB=AC
+C1=B1
=> ΔAEC = ΔADB
=> AE = AD
=>BCDE là hình thang cân
b) Ta có ∠ACB=∠ABC=50o(do BCDE là hình thang cân)
Ta có: ED//BC
\(\Rightarrow\left\{{}\begin{matrix}\widehat{ABC}=\widehat{AED}\\\widehat{ACB}=\widehat{ADE}\end{matrix}\right.=50^o}\) (SLT)
Mà ∠DEB=∠EDC
Ta có:
+∠DEB+∠AED=180o (kề bù)
=>50o+∠AED=180o
=>∠AED=180o-50o=130o
=>∠AED=∠ADE=130o

a) DDBC vuông có B C D ^ = 2 B D C ^ nên A D C ^ = B C D ^ = 60 0 và D A B ^ = C B A ^ = 120 0
b) Tính được DC = 2.BC = 12cm, suy ra PABCD = 30cm.
Hạ đường cao BK, ta có BK = 3 3 c m .
Vậy SABCD = 27 3 c m 2
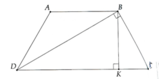

bạn tự vẽ hình nha!!
Ta có: gócBDC=gócABD(so le)
BDC^=ADB^ (gt BD là phân giác)
=>ABD^=ADB^
=> AD =AB =BC = a
mặt khác:
BDC^=1/2 ADC^ = 1/2 BCD^
mà BDC^ + BCD^ = 90*
=> BDC^ = 30*
=> CD = 2.BC = 2.a =
vậy chu vi hình thang là: a.3+2a =5a