Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

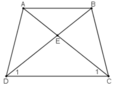
Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)
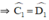
⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.

Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)
⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.

Do ABCD là hình thang cân nên AD = BC, AC = BC,
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, , DC là cạnh chung.
Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)
⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.

Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)
⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.

a) + Hình thang ABCD có EA = ED, FB = FC (gt)
⇒ EF là đường trung bình của hình thang ABCD.
⇒ EF // AB // CD
+ ΔABC có BF = FC (gt) và FK // AB (cmt)
⇒ AK = KC
+ ΔABD có: AE = ED (gt) và EI // AB (cmt)
⇒ BI = ID
b) + Vì EF là đường trung bình của hình thang ABCD.
⇒ EF = (AB + CD)/2 = (6 + 10)/2 = 8cm.
+ ΔABD có AE = ED, DI = IB
⇒ EI là đường trung bình của ΔABD
⇒ EI = AB/2 = 6/2 = 3(cm)
+ ΔABC có CF = BF, CK = AK
⇒ KF là đường trung bình của ΔABC
⇒ KF = AB /2 = 6/2 = 3cm
+ Lại có: EI + IK + KF = EF
⇒ IK = EF – EI – KF = 8 – 3 – 3 = 2cm
A B C D E F I K
A B C D E 1 1
Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
\(\Rightarrow\Delta ADC=\Delta BCD\left(c-c-c\right)\)
\(\Rightarrow\widehat{C_1}=\widehat{D_1}\)
=> ΔECD cân tại E
=> EC = ED.
Mà AC = BD
=> AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.

Do ABCD là hình thang cân nên AD = BC, AC = BC,
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, , DC là cạnh chung.
Hình hơi xấu!!!
A B C D E 1 1
Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
\(\Rightarrow\Delta ADC=\Delta BCD\left(c.c.c\right)\)
Suy ra góc C1 = góc D1
⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.
Chúc bạn học tốt !!!
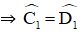
Bài giải:
Do ABCD là hình thang cân nên AD = BC, AC = BC, ˆD=ˆCD^=C^
Xét hai tam giác ADC và BCD, ta có: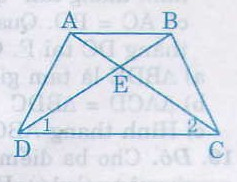
AD = BC (gt)
AC = BD (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra ˆC1=ˆD1C1^=D1^
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, ˆD=ˆCD^=C^ , DC là cạnh chung.