Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Xét △BCM: \(\left\{{}\begin{matrix}CI\perp MB\\BK\perp MC\\CI\cap BK=E\end{matrix}\right.\)
Suy ra E là trực tâm của △BCM
\(\Rightarrow ME\perp BC\)
b) Theo kết quả của câu a: \(ME\perp BC\)
Mà \(AB\perp BC\) (Vì ABCD là hình chữ nhật)
=> ME//AB
Lại có M là trung điểm AK
=> E là trung điểm BK
=> ME là đường trung bình của △AKB
\(\Rightarrow\left\{{}\begin{matrix}ME//AB\\ME=\dfrac{1}{2}AB\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}ME//NC\\ME=NC\end{matrix}\right.\)
=> MNCE là hình bình hành
=> Đpcm

a: 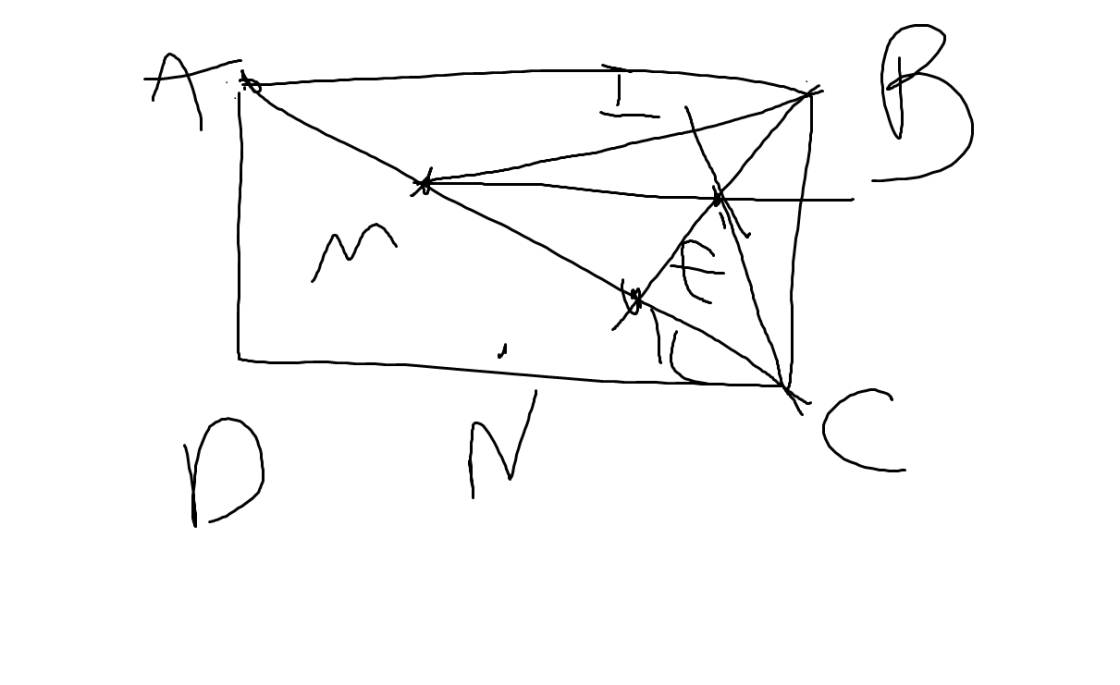
b: Xét ΔBMC có
BK,CI là các đường cao
BK cắt CI tại E
Do đó: E là trực tâm của ΔBMC
=>ME\(\perp\)BC
mà AB\(\perp\)BC
nên ME//AB
Xét ΔKAB có
M là trung điểm của KA
ME//AB
Do đó: E là trung điểm của BK
=>BE=EK
c: Xét ΔKAB có
M,E lần lượt là trung điểm của KA,KB
=>ME là đường trung bình của ΔKAB
=>\(ME=\dfrac{AB}{2}\)
mà AB=CD(ABCD là hình chữ nhật)
và \(NC=\dfrac{CD}{2}\)(N là trung điểm của CD)
nên ME=NC
Ta có: ME//AB
CD//AB
Do đó: ME//CD
Xét tứ giác MNCE có
ME//CN
ME=CN
Do đó: MNCE là hình bình hành
d: ta có: MNCE là hình bình hành
=>MN//CE
mà CE\(\perp\)MB
nên MN\(\perp\)MB

Hình em tự vẽ nha.
a, ABCD là hình bình hành \(\Rightarrow\)2 đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường
Tứ giác AHCK có 2 đường chéo AC và HK tại trung điểm của mỗi đường \(\Rightarrow\)AHCK là hình bình hành
b, AHCK là hình bình hành \(\Rightarrow AH//CK\Leftrightarrow AM//NC\)
Tứ giác AMCN có: \(AN//MC\left(gt\right)\)
\(AM//NC\left(cmt\right)\)
\(\Rightarrow\)AMCN là hình bình hành \(\Rightarrow\)2 đường chéo AC và MN cắt nhau tại trung điểm O của AC \(\Rightarrow\)O là trung điểm của MN

a)xét tứ giác ADME có
CÂB =AÊM=góc ADM=900
=>ADME là hcn
b)vì MA là đg trung tuyến nên MA=MC=MB
xét tam giác CMA có
CM=MA(cmt)
CÊM=AÊM=900
EM là cạnh chung
=>...(cạnh huyền-cạnh góc vuông)
=>CE=EA
mà EA=MD(EAMD là hcn) nên CE=MD (1)
ta có MA=MC(cmt)
mà MA=ED(EAMD là hcn)
=>MC=ED (2)
xét tứ giác CMDE có CE=MD,CM=ED( 1 và 2)
=>CMED là hbh
c)
xét tam giác MDB vuông tại D có DI là trung tuyến nên MI=IB=ID
xét tứ giác MKDI có
KM=KD(K là giao điểm hai dg chéo của hcn)
KM=MI(vì MA=MB mà K và I lần lượt là trung điểm của chúng)
MI=ID(cmt)
=>KMID là thoi
mà KI là đg chéo của góc I nên KI cũng là p/g của góc I
(ck hk tốt nhé)