Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, gọi MN cắt BC tại O
xét tam giácBDC có : M là trung điểm của BD (gt)
MO // DC (Gt)
=> O là trung điểm của BC (đl)
xét tam giác ABC có : NO // AB
=> N là trung điểm của AB (đl)

a/ Cho MN giaco AD,BC tại H,K
\(\Delta ABD\) có : M là tđ BD, HM//AB\(\Rightarrow\) H là tđ AD(1)
\(\Delta BDC\) có : M là tđ BD, MK//DC\(\Rightarrow\) K là tđ BC(2)
Từ (2) và NK//AB suy ra N là tđ AC

A B C D M N Q P
từ MN kẻ đt đi qua BC, AD, cắt BC và AD lần lượt tại P, Q
a)
Xét tam giác BCD có :
M là tđ của BD
MP//CD (P thuộc MN, MN//CD)
=> P là tđ của BC( t/c đtb)
Xét tam giác ABC có:
P là tđ của BC( cmt)
NP//AB (AB//CD,MN//CD, P thuộc MN)
=> N là tđ của AC (đpcm)
b)
Xét tam giác ABD có:
M là tđ của BD
MQ//AB ( Q thuộc MN, MN//AB)
=> Q là tđ của AD
=> MQ là đtb của tam giác ABD
Xét hình thang ABCD có:
P là tđ của BC
Q là tđ của AD
=> PQ là đtb của hình thang ABCD
theo cm câu a và b ta có:
PQ=\(\frac{AB+CD}{2}\) , PN=\(\frac{AB}{2}\), MQ= \(\frac{AB}{2}\)
lại có :
MN = PQ - PN - MQ
=> MN= \(\frac{AB+CD}{2}-\frac{AB}{2}-\frac{AB}{2}\) = \(\frac{AB+CD-AB-AB}{2}\) = \(\frac{CD-AB}{2}\) (đpcm)
( do hình trong vở và ở đây khác nhau nên co thể sẽ có một vài chỗ sai sót)

A B C D N M E
a, kẻ AM cắt CD tại E
xét tam giác AMB và tam giác EMD có : góc AMB = góc EMD (đối đỉnh)
DM = MB do M là trung điểm của BD (gt)
góc ABM = góc MDE (so le trong AB // DC)
=> tam giác AMB = tam giác EMD (g-c-g) (1)
=> AM = ME (đn) có M nằm giữa A và E
=> M là trung điểm của AE
N là trugn điểm của AC (gt) ; xét tam giác AEC
=> MN là đường trung bình của tam giác AEC (đn) (2)
=> MN // EC (Đl)
CE // AB
=> MN // AB
b, (2) => MN = EC/2
EC = CD - DE
=> MN = (CD - DE) : 2
(1) => DE = AB
=> MN = (CD - AB) : 2

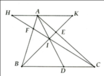
a, Kéo dài BN cắt CD tại G.
Xét \(\Delta BDG:\)
M là trung điểm BD
MN // CD
\(\Rightarrow\)N là trung điểm BG hay N là trung điểm AC.
b,Xét \(\Delta ANB\) và \(\Delta CNG:\)
AN = NC (cmt )
\(\widehat{ANB}=\widehat{CNG}\)( đối đỉnh )
Vì AB // CD nên \(\widehat{BAN=\widehat{GCN}}\)
\(\Rightarrow\Delta ANB=\Delta CNG\left(g-c-g\right)\)
\(\Rightarrow AB=GC;BN=NG\)( 2 cặp cạnh tương ứng )
Xét \(\Delta BDG:\)
M là trung điểm BD
N là trung điểm BG
\(\Rightarrow\)MN là đường trung bình của \(\Delta BDG\)
\(\Rightarrow MN//DG;MN=\frac{1}{2}DG\)
Ta lại có : \(MN=\frac{1}{2}DG\)
\(\Rightarrow MN=\frac{1}{2}\left(DC-GC\right)\)
\(\Leftrightarrow MN=\frac{DC-AB}{2}\)( Vì AB = GC )