Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1]
a]
Ta có:
AI/IM = AB/DM
BK/KM = AB/MC
Do DM =MC
=> AI/IM = BK/KM
=> IK//AB
b]
IE/DM = AI/AM
KF/MC = BK/BM
Mà AI/AM = BK/BM (do IK//AB)
=> IE/DM = KF/MC mà DM=MC
=> IE = KF
2]
a}
Ta có:
AE/EK = AB/DK
BF/FI = AB/CI
Do ABID và ABCK là h..b.hành
=> CK=DI =AB
=> DK = CI = CD -AB
=> AE/EK = NF/FI
=> EF//AB
b}
Ta có EF/CK =AF/AC = AB/CD
=> EF.CD = CK.AB = AB^2 (do CK =AB)
3]
a}
Ta có:
MB/MF = MC/MA (Xét BC//AF)
ME/MB = MC/MA (Xét CE//AB)
=> MB/MF = ME/MB
=> MB^2 = ME.MF
b}
BM/MF = MC/AC (Xét BC//AF)
BM/ME = AM/AC (Xét CE//AB)
=> BM/MF + BM/ME = MC/AC + AM/AC =1
=> BM/MF + BM/ME =1
=> 1/BF+1/BE=1/BM

Ta có E và F là trung điểm của AD và BC
=> EF là ĐTB của hình thang ABCD
=> EF//AB//CD
Do F,K là trung điểm cuả BD và BC
=> FK là ĐTB của tam giác ADC
=> FK//CD
Do E và K là trung điểm của AD và BD
=> EK là ĐTB của tam giác ABD
=> EK//AB
Mà AB//CD
=>EF ; EK ; FK cùng // với AB
=> E ; F ; K thẳng hàng

Bài giải:
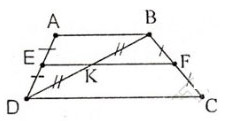
Ta có EA = ED, KB = KD (gt)
Nên EK // AB
Lại có FB = FC, KB = KD (gt)
Nên KF // DC // AB
Qua K ta có KE và KF cùng song song với AB nên theo tiên đề Ơclit ba điểm E, K, F thẳng hàng.
\(\Delta ADB\) có:\(AE=DE\left(gt\right),BF=FD\left(gt\right)\)
\(\Rightarrow AB\) // \(EF\)(theo đlí 2 về đường trung bình của tam giác) (1)
\(\Delta BDC\) có:\(BK=KC\left(gt\right),BF=FD\left(gt\right)\)
\(\Rightarrow FK\) // \(CD\)(theo đlí 2 về đường trung bình của tam giác)
Mà \(CD\) // \(AB\Rightarrow FK\) // \(AB\) (1)
Từ (1) và (2), suy ra:
\(AB\) // \(EF,FK\)
\(\Rightarrow E,F,K\) thẳng hàng (theo tiên đề Ơclit )

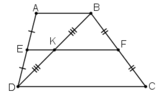
+ ΔABD có DE = EA và DK = KB
⇒ EK là đường trung bình của ΔDAB
⇒ EK // AB
+ Hình thang ABCD có: AE = ED và BF = FC
⇒ EF là đường trung bình của hình thang ABCD
⇒ EF // AB// CD
+ Qua điểm E ta có EK // AB và EF // AB nên theo tiên đề Ơclit ta có E, K, F thẳng hàng.

Xét ΔDAB có
E là trung điểm của AD
K là trung điểm của BD
Do đó: EK//AB
hay EK//CD
Xét ΔBDC có
K là trung điểm của BD
F là trung điểm của BC
Do đó: KF là đường trung bình của ΔBDC
Suy ra: KF//DC
Ta có: EK//DC
KF//DC
mà KE và KF có điểm chung là K
nên E,K,F thẳng hàng
A B C D I M K
Trong \(\Delta ABC\) có \(AK=KC\left(gt\right)\)và \(BM=MC\left(gt\right)\)
\(\Rightarrow KM\)là đường trung bình của \(\Delta ABC\)
\(\Rightarrow KM//AB\)\(\left(1\right)\)
Trong \(\Delta BDC\)có \(BI=ID\left(gt\right)\)và \(BM=MC\left(gt\right)\)
\(\Rightarrow IM\)là đường trung bình của \(\Delta BDC\)
\(\Rightarrow IM//DC\)
Mà \(DC//AB\)\(\Rightarrow IM//AB\)\(\left(2\right)\)
Từ ( 1 ) và ( 2 ) \(\Rightarrow I,M,K\)thẳng hàng ( tiên đề Ơ - clit )