Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
i: \(AD=\sqrt{24^2-12^2}=12\sqrt{3}\left(cm\right)\)
\(AO=\dfrac{12\cdot12\sqrt{3}}{24}=6\sqrt{3}\left(cm\right)\)
\(BO=\dfrac{AB^2}{BD}=\dfrac{12^2}{24}=6\left(cm\right)\)
DO=24-6=18cm

A B C D 5 12 H K N
a) Ta có: Áp dụng định lý Pytago:
\(AC^2=AB^2+BC^2=5^2+12^2=169\)
\(\Rightarrow AC=13\left(cm\right)\)
Áp dụng định lý thứ 4 ta có:
\(\frac{1}{BH^2}=\frac{1}{AB^2}+\frac{1}{BC^2}=\frac{1}{5^2}+\frac{1}{12^2}\)
\(\Leftrightarrow BH^2=\frac{3600}{169}\Rightarrow BH=\frac{60}{13}\left(cm\right)\)
Ta có: ΔAHN ~ ΔKDN (g.g)
=> \(\frac{AN}{NH}=\frac{KN}{ND}\Leftrightarrow HN\cdot NK=AN\cdot ND\) (1)
Lại có: ΔAHN ~ ΔADC (g.g)
=> \(\frac{AN}{AH}=\frac{AC}{AD}\Leftrightarrow\frac{AN}{AH}=\frac{HC}{ND}\Rightarrow AN\cdot ND=AH\cdot HC\) (2)
Từ (1) và (2) => \(AH\cdot HC=HN\cdot NK\Leftrightarrow BH^2=HN.NK\)
=> đpcm

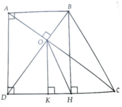
a, Tính được DB=15cm. A D B ^ ≈ 37 0 ; A B D ^ ≈ 53 0
b, Tính được AO=7,2cm, DO=9,6cm và AC=20cm
c, Kẻ OK ⊥ DC tại K
DH=AB=9cm, DC=16cm, DK=5,76cm và OK=7,68cm
Từ đó S D O H = O K . D H 2 = 7 , 68 . 9 2 = 34,56 c m 2
a: \(AD=\sqrt{24^2-12^2}=12\sqrt{3}\left(cm\right)\)
\(AO=\dfrac{12\cdot12\sqrt{3}}{24}=6\sqrt{3}\left(cm\right)\)
\(DO=\dfrac{AD^2}{DB}=\dfrac{\left(12\sqrt{3}\right)^2}{24}=\dfrac{144\cdot3}{24}=18\left(cm\right)\)
OB=24-18=6cm
b: \(BH^2+MH^2=BM^2\)(ĐỊnh lí Pytago)
mà \(BM^2=MH\cdot MC\)(Hệ thức lượng)
nên \(BH^2+MH^2=MH\cdot MC\)