Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ABCDaaKH
a) Hình thang ABCD có : \(\widehat{A}\) \(=\) \(\widehat{D}\) \(=\) \(90^0\)
Kẻ \(BH\perp CD\)
=> ABHD là hình chữ nhật \((\widehat{A}=\widehat{D}=\widehat{H}=90^0)\)
Có AB = AD = a
=> ABHD là hình vuông .
=> AB = AD = BH = DH = a
=> HC = DC - HD = 2a - a = a
\(\Delta BHC\) có \(\widehat{A}=90^0\)
\(\Rightarrow\) \(tanC=\frac{BH}{HC}=\frac{a}{a}=1\)
b) \(S_{ABCD}=\frac{\left(AB+CD\right)AD}{2}=\frac{3a^2}{2}\)
\(S_{DBC}=\frac{1}{2}BH.CD=\frac{1}{2}.a.2a=a^2\)
\(\frac{S_{DBC}}{S_{ABCD}}=\frac{a^2}{\frac{3a^2}{2}}=\frac{2}{3}\)
c) Kẻ \(KC\perp AB\)
=> AD = CK = a
\(S_{ABC}=\frac{1}{2}CK.AB=\frac{1}{2}a.a=\frac{a^2}{2}\)
\(\frac{S_{ABC}}{S_{DBC}}=\frac{\frac{a^2}{2}}{a^2}=\frac{1}{2}\)

AB=21/(3+4)x3=9 cm
AC=21-9=12cm
Tự kẻ hình bạn nhé =)))
Áp dụng định lí Pitago vào tam giác ABC , có
AB^2+AC^2=BC^2
=>thay số vào, tính được BC=15cm
Áp dụng hệ thức giữa cạnh và đường cao trong tg vuông, có:
AB^2=BHxBC
=>BH=81/15=5.4cm
=>CH=15-5.4=9.6cm
AH^2=BHxCH=5.4x9.6=51.84cm

Ủa sao lại 2 tam giác hay 2 tứ giác nhỉ? BE chia hình thang thành 1 tam giác và 1 tứ giác chứ?
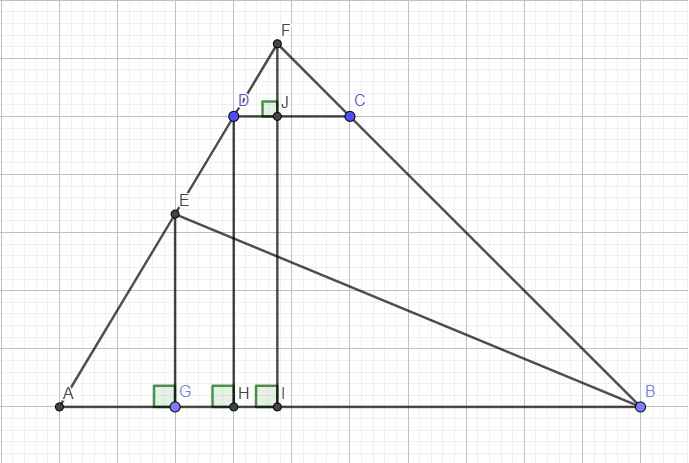
Hướng dẫn là em kéo dài AD và BC cắt nhau tại F. Sử dụng định lý Talet
\(\dfrac{DF}{AF}=\dfrac{CD}{AB}=\dfrac{1}{5}\) \(\Rightarrow\dfrac{DF}{AD}=\dfrac{1}{4}\) ; \(\dfrac{AD}{AF}=\dfrac{4}{5}\)
\(EA=3DE\Rightarrow\dfrac{AE}{AD}=\dfrac{3}{4}\Rightarrow\dfrac{AE}{AF}=\dfrac{3}{5}\)
Từ E, D, F hạ vuông góc xuống AB tại G, H, I, FI cắt CD tại J
Talet: \(FJ=\dfrac{1}{5}FI\) ; \(\dfrac{DH}{FI}=\dfrac{AD}{AF}=\dfrac{4}{5}\Rightarrow DH=\dfrac{4}{5}FI\) ; \(\dfrac{EG}{FI}=\dfrac{AE}{AF}=\dfrac{3}{5}\Rightarrow EG=\dfrac{3}{5}FI\)
\(S_{ABF}=\dfrac{1}{2}FI.AB\)
\(S_{DCF}=\dfrac{1}{2}FJ.DC=\dfrac{1}{2}.\dfrac{1}{5}FI.\dfrac{1}{5}AB=\dfrac{1}{25}\left(\dfrac{1}{2}FI.AB\right)=\dfrac{1}{25}S_{ABF}\)
\(\Rightarrow S_{ABCD}=S_{ABF}-S_{CDF}=\dfrac{24}{25}S_{ABF}\)
\(S_{ABE}=\dfrac{1}{2}EG.AB=\dfrac{1}{2}.\dfrac{3}{5}FI.AB=\dfrac{3}{5}S_{ABF}\)
\(\Rightarrow S_{BCDE}=S_{ABCD}-S_{ABE}=\dfrac{24}{25}S_{ABF}-\dfrac{3}{5}S_{ABF}=\dfrac{9}{25}S_{ABF}\)
\(\Rightarrow\dfrac{S_{ABE}}{S_{BCDE}}=\dfrac{\dfrac{3}{5}S_{ABF}}{\dfrac{9}{25}S_{ABF}}=\dfrac{5}{3}\)
Chi tiết phân giác góc B thừa, ko cần sử dụng

**a) Chứng minh OMBN nội tiếp:** Trong hình thang cân ABCD, ta có AB // CD và ∠A = ∠B = 60°. Vì đường tròn nội tiếp tiếp xúc với AB, BC tại M, N, ta có OM ⊥ AB và ON ⊥ BC. Do đó, ∠OMB = ∠ONB = 90°. Xét tứ giác OMBN: ∠OMB + ∠ONB = 90° + 90° = 180°. Vì tổng hai góc đối diện bằng 180°, tứ giác OMBN nội tiếp. **b) Chứng minh AD, BC, MP đồng quy:** Vì ABCD là hình thang cân, nên AD = BC. Gọi I là giao điểm của AD và BC. Ta cần chứng minh I nằm trên MP. Trong hình thang cân, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường. Gọi giao điểm của AC và BD là K. K là trung điểm của AC và BD. Do đường tròn nội tiếp tiếp xúc với AB, CD tại M, P, ta có AM = AP. Tương tự, BM = BN và DP = DQ. Xét tam giác AMP và tam giác BMN: * AM = AP * BM = BN * ∠A = ∠B = 60° Tuy nhiên, ta không thể khẳng định hai tam giác này bằng nhau. Cần thêm thông tin để chứng minh AD, BC, MP đồng quy. Phương pháp chứng minh này không đủ mạnh. Cần xem xét các tính chất khác của hình thang cân và đường tròn nội tiếp. **c) Tính QN và chu vi SDC theo a:** Vì ABCD là hình thang cân với ∠A = ∠B = 60°, nên ABCD là hình thang cân có đáy lớn AB và đáy nhỏ CD. Ta có AB = a. Do đường tròn nội tiếp tiếp xúc với các cạnh, ta có: * AM = AQ * BM = BN * CP = CQ * DP = DM AM + MB = AB = a AQ + QD = AD CP + PD = CD BN + NC = BC Vì hình thang cân, AD = BC. Tuy nhiên, không đủ thông tin để tính QN và chu vi SDC chỉ dựa trên AB = a. Cần thêm thông tin về chiều cao hoặc độ dài CD. **d) Tính tỉ số S1/S2:** Gọi h là chiều cao của hình thang. Diện tích tam giác SAB là: S2 = (1/2) * AB * h = (1/2) * a * h Diện tích tam giác SDC là: S1 = (1/2) * CD * h Tỉ số S1/S2 = (CD/AB) Vì không có thông tin về độ dài CD, ta không thể tính tỉ số S1/S2. **Kết luận:** Chỉ có phần a) được chứng minh hoàn toàn. Các phần b), c), d) cần thêm thông tin hoặc phương pháp chứng minh khác để giải quyết. Cần xem xét lại đề bài hoặc cung cấp thêm dữ kiện để giải quyết hoàn chỉnh các phần còn lại.

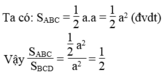
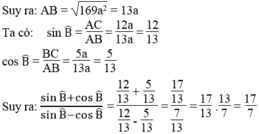
A B a a D a H a C I
a. Kẻ \(BH\perp CD\)
Ta có: AB // CD và góc A = 90o
Suy ra:góc D = 90o
Tứ giác ABHD có 3 góc vuông và AB = AD = a nên là hình vuông
Suy ra: DH = BH = AB = a
Ta có: CD = DH + HC
Suy ra: HC = CD – DH = 2a – a = a
Vậy \(tg\widehat{C}=\frac{BH}{CH}=aa=1\)
b)
Ta có :
\(S_{BCD}=\frac{1}{2}BH.CD=\frac{1}{2}a.2a=a^2\left(đvdt\right)\)
\(S_{ABCD}=\frac{AB+CD}{2}.AD=\frac{a+2a}{2}.a=\frac{3}{2}a^2\left(đvdt\right)\)
Vậy : \(\frac{S_{BCD}}{S_{ABCD}}=\frac{a^2}{\frac{3}{2}a^2}=\frac{1}{\frac{3}{2}}=\frac{2}{3}\)
c)
Ta có : \(S_{ABC}=\frac{1}{2}a.a=\frac{1}{2}a^2\left(đvdt\right)\)
Vậy : \(\frac{S_{ABC}}{S_{BCD}}=\frac{\frac{1}{2}a^2}{a^2}=\frac{1}{2}\)