Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B a a D a H a C I
a. Kẻ \(BH\perp CD\)
Ta có: AB // CD và góc A = 90o
Suy ra:góc D = 90o
Tứ giác ABHD có 3 góc vuông và AB = AD = a nên là hình vuông
Suy ra: DH = BH = AB = a
Ta có: CD = DH + HC
Suy ra: HC = CD – DH = 2a – a = a
Vậy \(tg\widehat{C}=\frac{BH}{CH}=aa=1\)
b)
Ta có :
\(S_{BCD}=\frac{1}{2}BH.CD=\frac{1}{2}a.2a=a^2\left(đvdt\right)\)
\(S_{ABCD}=\frac{AB+CD}{2}.AD=\frac{a+2a}{2}.a=\frac{3}{2}a^2\left(đvdt\right)\)
Vậy : \(\frac{S_{BCD}}{S_{ABCD}}=\frac{a^2}{\frac{3}{2}a^2}=\frac{1}{\frac{3}{2}}=\frac{2}{3}\)
c)
Ta có : \(S_{ABC}=\frac{1}{2}a.a=\frac{1}{2}a^2\left(đvdt\right)\)
Vậy : \(\frac{S_{ABC}}{S_{BCD}}=\frac{\frac{1}{2}a^2}{a^2}=\frac{1}{2}\)

Ủa sao lại 2 tam giác hay 2 tứ giác nhỉ? BE chia hình thang thành 1 tam giác và 1 tứ giác chứ?
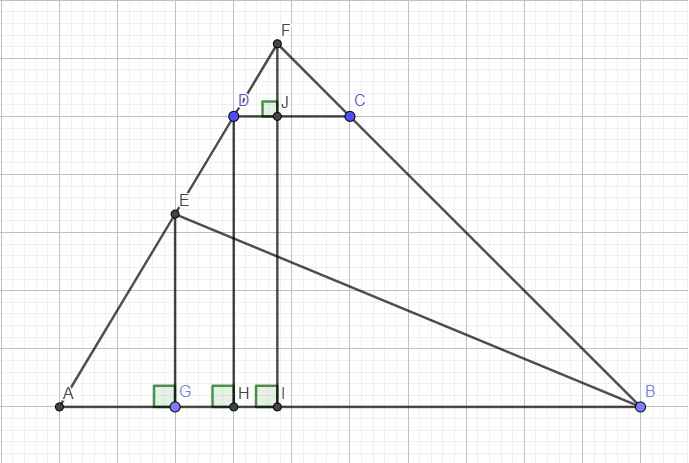
Hướng dẫn là em kéo dài AD và BC cắt nhau tại F. Sử dụng định lý Talet
\(\dfrac{DF}{AF}=\dfrac{CD}{AB}=\dfrac{1}{5}\) \(\Rightarrow\dfrac{DF}{AD}=\dfrac{1}{4}\) ; \(\dfrac{AD}{AF}=\dfrac{4}{5}\)
\(EA=3DE\Rightarrow\dfrac{AE}{AD}=\dfrac{3}{4}\Rightarrow\dfrac{AE}{AF}=\dfrac{3}{5}\)
Từ E, D, F hạ vuông góc xuống AB tại G, H, I, FI cắt CD tại J
Talet: \(FJ=\dfrac{1}{5}FI\) ; \(\dfrac{DH}{FI}=\dfrac{AD}{AF}=\dfrac{4}{5}\Rightarrow DH=\dfrac{4}{5}FI\) ; \(\dfrac{EG}{FI}=\dfrac{AE}{AF}=\dfrac{3}{5}\Rightarrow EG=\dfrac{3}{5}FI\)
\(S_{ABF}=\dfrac{1}{2}FI.AB\)
\(S_{DCF}=\dfrac{1}{2}FJ.DC=\dfrac{1}{2}.\dfrac{1}{5}FI.\dfrac{1}{5}AB=\dfrac{1}{25}\left(\dfrac{1}{2}FI.AB\right)=\dfrac{1}{25}S_{ABF}\)
\(\Rightarrow S_{ABCD}=S_{ABF}-S_{CDF}=\dfrac{24}{25}S_{ABF}\)
\(S_{ABE}=\dfrac{1}{2}EG.AB=\dfrac{1}{2}.\dfrac{3}{5}FI.AB=\dfrac{3}{5}S_{ABF}\)
\(\Rightarrow S_{BCDE}=S_{ABCD}-S_{ABE}=\dfrac{24}{25}S_{ABF}-\dfrac{3}{5}S_{ABF}=\dfrac{9}{25}S_{ABF}\)
\(\Rightarrow\dfrac{S_{ABE}}{S_{BCDE}}=\dfrac{\dfrac{3}{5}S_{ABF}}{\dfrac{9}{25}S_{ABF}}=\dfrac{5}{3}\)
Chi tiết phân giác góc B thừa, ko cần sử dụng

AB=21/(3+4)x3=9 cm
AC=21-9=12cm
Tự kẻ hình bạn nhé =)))
Áp dụng định lí Pitago vào tam giác ABC , có
AB^2+AC^2=BC^2
=>thay số vào, tính được BC=15cm
Áp dụng hệ thức giữa cạnh và đường cao trong tg vuông, có:
AB^2=BHxBC
=>BH=81/15=5.4cm
=>CH=15-5.4=9.6cm
AH^2=BHxCH=5.4x9.6=51.84cm

a) Xét tam giác AOD và tam giác BAD có:
{Dˆ:chungAOˆD=DAˆB=90{D^:chungAO^D=DA^B=90⇒ΔAOD≀ΔBAD(g.g)⇒ΔAOD≀ΔBAD(g.g)
b) Ta có: DAˆO=ABˆD=ABˆO(ΔAOD≀ΔBAD)DA^O=AB^D=AB^O(ΔAOD≀ΔBAD)
Và AOˆD=AOˆB=90AO^D=AO^B=90 (2 đường chéo vuông góc tại O)
Do đó ΔAOD≀ΔBOA(g.g)ΔAOD≀ΔBOA(g.g)
⇒ADAB=ODAO⇒ADAB=ODAO (1)
Lại có: {DAˆO:chungAOˆD=ADˆC=90{DA^O:chungAO^D=AD^C=90⇒ΔADC≀ΔAOD(g.g)⇒ΔADC≀ΔAOD(g.g)
⇒CDOD=ADAO⇔CDAD=ODAO⇒CDOD=ADAO⇔CDAD=ODAO (2)
Từ (1);(2)⇒ADAB=CDAD⇒AD2=AB⋅CD⇒ADAB=CDAD⇒AD2=AB⋅CD
c) Ta có: AB song song với DC (ABCD là hình thang)
⇒ABˆO=ODˆC(slt)⇒AB^O=OD^C(slt)
Và AOˆB=DOˆC(đ2)AO^B=DO^C(đ2)
Do đó ΔOCD≀ΔOAB(g.g)ΔOCD≀ΔOAB(g.g)
⇒k=OCOA=CDAB=94⇒k=OCOA=CDAB=94
⇒SΔOCDSΔOAB=k2=942=8116⇒SΔOCDSΔOAB=k2=942=8116
Vậy........................
Δ : tam giác. Chúc bạn học tốt nhé!

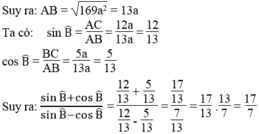
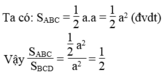
ABCDaaKH
a) Hình thang ABCD có : \(\widehat{A}\) \(=\) \(\widehat{D}\) \(=\) \(90^0\)
Kẻ \(BH\perp CD\)
=> ABHD là hình chữ nhật \((\widehat{A}=\widehat{D}=\widehat{H}=90^0)\)
Có AB = AD = a
=> ABHD là hình vuông .
=> AB = AD = BH = DH = a
=> HC = DC - HD = 2a - a = a
\(\Delta BHC\) có \(\widehat{A}=90^0\)
\(\Rightarrow\) \(tanC=\frac{BH}{HC}=\frac{a}{a}=1\)
b) \(S_{ABCD}=\frac{\left(AB+CD\right)AD}{2}=\frac{3a^2}{2}\)
\(S_{DBC}=\frac{1}{2}BH.CD=\frac{1}{2}.a.2a=a^2\)
\(\frac{S_{DBC}}{S_{ABCD}}=\frac{a^2}{\frac{3a^2}{2}}=\frac{2}{3}\)
c) Kẻ \(KC\perp AB\)
=> AD = CK = a
\(S_{ABC}=\frac{1}{2}CK.AB=\frac{1}{2}a.a=\frac{a^2}{2}\)
\(\frac{S_{ABC}}{S_{DBC}}=\frac{\frac{a^2}{2}}{a^2}=\frac{1}{2}\)