Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C 3 4 H I D
a, C/m ΔABC ∼ ΔHAC ⇒ AC2 = CH . BC
Xét ΔvABC và ΔvHAC. Ta có: \(\widehat{ACB}\) chung (gt)
⇒ ΔABC ∼ ΔHAC
Nên: \(\frac{AC}{CH}=\frac{BC}{AC}\)
⇒ AC2 = CH . BC
b, Tính AD, DB?
Ta có: ΔABC vuông tại A (gt)
⇒ BC2 = AB2 + AC2 = 32 + 42 = 25
Nên: BC = \(\sqrt{25}=5\left(cm\right)\)
Mà: CD là tia phân giác của \(\widehat{ACB}\) (gt)
⇒ \(\frac{AD}{AC}=\frac{DB}{BC}\)
Nên: \(\frac{AD}{AC}=\frac{DB}{BC}=\frac{AD+DB}{AC+BC}=\frac{AB}{AC+BC}\)
Hay: \(\frac{AD}{4}=\frac{DB}{5}=\frac{3}{4+5}=\frac{1}{3}\)
⇒ \(AD=\frac{4}{3}\left(cm\right)\)
\(DB=\frac{5}{3}\left(cm\right)\)
Cho hình chữ nhật ABCD. Vẽ AH vuông góc BD (H\(\in\)BD), HK//CD (K\(\in\)BC).
a) CM: tam giác ADH đồng dạng với tam giác DBC
b) CM: CD.BK=AH.BH
c) Cho biết AB=5cm, HB=4cm. Tính BK?

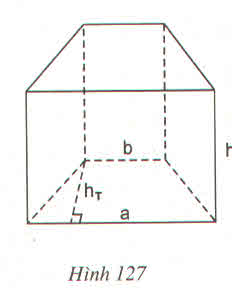
diện tích xung quanh của lăng trụ là (\(\sqrt{53}\times2+11+15)\)\(\times\)14\(\approx\)567,8mm2

Bài 1:
Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
DO đó: F là trung điểm của AC
Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình
=>EF//BC
hay BEFC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BEFC là hình thang cân

Bài 1
a) Xét tam giác BCD có BM=MD(gt), BN=NC(gt) => MN là đg` TB => MN// DC => MN// DE(1)
và MN=1/2DC => MN= DE(2)
từ (1)và (2) => MNED là hbh
b) MNED là hbh(câu a) => MD//NE => ADM= DEN(đồng vị)
Xét tam giác ABD vg tại A có BM=DM=> AM là trung tuyến => AM=1/2BD= MD
=> tam giác ADM cân tại M => MDA = DAM
=> DEN= MAD (3)
MN//DE=> MN//AE => AMNE là hình thang (4)
từ (3)và (4) => AMNE là hình thang cân
c) để MNED là hình thoi \Leftrightarrow MNED là hbh có MD=DE \Leftrightarrow 1/2BD=1/2CD \Leftrightarrow BD = CD \Leftrightarrow tam giác BCD cân tại D \Leftrightarrow DBC=góc C \Leftrightarrow góc C=1/2góc B\Leftrightarrow góc C=2góc B
Vậy để MNED là hình thoi thì tam giác ABC có góc C=2góc B
- Bài 1
a) Xét tam giác BCD có BM=MD(gt), BN=NC(gt) => MN là đg` TB => MN// DC => MN// DE(1)
và MN=1/2DC => MN= DE(2)
từ (1)và (2) => MNED là hbh
b) MNED là hbh(câu a) => MD//NE => ADM= DEN(đồng vị)
Xét tam giác ABD vg tại A có BM=DM=> AM là trung tuyến => AM=1/2BD= MD
=> tam giác ADM cân tại M => MDA = DAM
=> DEN= MAD (3)
MN//DE=> MN//AE => AMNE là hình thang (4)
từ (3)và (4) => AMNE là hình thang cân
c) để MNED là hình thoi \Leftrightarrow MNED là hbh có MD=DE \Leftrightarrow 1/2BD=1/2CD \Leftrightarrow BD = CD \Leftrightarrow tam giác BCD cân tại D \Leftrightarrow DBC=góc C \Leftrightarrow góc C=1/2góc B\Leftrightarrow góc C=2góc B
Vậy để MNED là hình thoi thì tam giác ABC có góc C=2góc Bnhuquynhdat, 17 Tháng mười hai 2013#2 
nhuquynhdatGuest
bài 2
a) AB//CD => AB//CE(1)
Xét tam giác ADE có AH là đg` cao
lại có E đối xứng với D qua H => H là trung điểm của DE => AH là trung tuyến
=> tam giác ADE cân tại A
=> ADE=AED(goác đáy tam giác cân)
mặt khác ABCD là hình thang cân => ADC=góc C
=> góc C= AED
mà 2 góc này ở vị trí đồng vị của AE và BC => AE//BC(2)
từ (1)và (2) => ABCE là hbh
b) xét tam giác AHE và tam giác FHD có góc AHE=góc DHF(đối đỉnh)
DH=HE(gt)
AE//DF(gt)=> AEH=FDH(SLT)
=>tam giác AHE=tam giác FHD(gcg) => AH=HF => H là TĐ của AF
c) Ta có AH=HF(câu b)DH=HE(gt) => ADFE là hbh
mà AH vg góc với ED=> AF vg góc với ED => ADEF là hình thoi
lại có tam giác ADE cân tại A (câu a)=> AD=AE => ADEF là hình vg
Chu vi đáy là:
P = 2(AB + BC) = 2.(6 + 4) = 20cm
Diện tích xung quanh của hình lăng trụ đã cho là:
S x q = P . h = 20 . 5 = 100 ( c m 2 )
Chọn đáp án A