

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



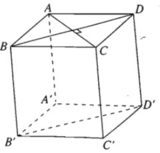
Từ giả thiết suy ra tứ giác ABCD là hình thoi, do đó AC ⊥ BD
Dễ thấy mặt chéo BDD'B' của hình hộp đã cho là hình bình hành, do đó BD // B′D′. Từ đó, theo bài 3.12 suy ra AC ⊥ B'D'.

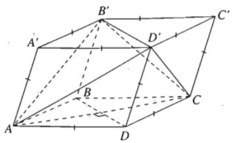
Theo giả thiết các mặt của hình hộp đều là hình thoi.
Ta có ABCD là hình thoi nên AC ⊥ BD
Theo tính chất của hình hộp: BD // B'D', do đó AC ⊥ B'D'.
Chứng minh tương tự ta được AB' ⊥ CD', AD' ⊥ CB'
Hai mặt phẳng (AA'C'C) và (BB'D'D) vuông góc với nhau khi hình hộp ABCD.A'B'C'D'là hình lập phương.


Trước hết dễ thấy tứ giác A'B'CD là hình bình hành, ngoài ra B′C = a = CD nên nó là hình thoi. Ta chứng minh hình thoi A'B'CD là hình vuông. Ta có:
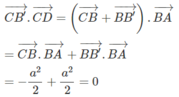
Vậy tứ giác A’B’CD là hình vuông.

Lời giải:
a) Tứ giác DBB'D' là hình bình hành nên BD // B'D' . Vì vậy BD // (B'D'C) và BA' // CD' \(\Rightarrow\) BA' // ( B'D'C).
Từ đó suy ra ( BDA') //B'D'C).
b) Gọi ,
là giao điểm của AC' với A'O và CO'.
Do \(G_1=A'O\cap AI\) và A'O và AI là hai đường trung tuyến của tam giác nên \(G_1\) là trọng tâm của tam giác A'AC.
Chứng minh tương tự \(G_2\) là trọng tâm tam giác CAC'.
Suy ra \(\dfrac{AG_1}{AO}=\dfrac{2}{3}\); \(\dfrac{CG_2}{CO}=\dfrac{2}{3}\) nên đường chéo AC' đi qua trọng tâm của hai tam giác BDA' và B'D'C.
c) Do O và O' lần lượt là trung điểm của AC và A'C' nên \(OC=A'O'\) và OC' // A'O'.
Vì vậy tứ giác OCO'A là hình bình hành và OA'//OC.
Từ đó ta chứng minh được \(G_1\) lần lượt là trung điểm của \(AG_1\) và \(G_2\) là trung điểm của \(G_1C'\).
Do đó: \(AG_1=G_1G_2=G_2C\) (đpcm).
d) \(\left(A'IO\right)=\left(AA'C'C\right)\). Nên thiết diện cần tìm là (AA'C'C).

+) Vì hình hộp ABCD.A'B'C'D' có các cạnh bằng nhau nên tứ giác A'B'C'D'; ADD'A'; CC'D'D là hình thoi.
+) AB' // C'D và C'D \( \bot \) CD' nên AB' \( \bot \)CD'
+) AC // A'C' và A'C' \( \bot \) B'D' nên AC \( \bot \) B'D'
+) B'C // A'D và A'D \( \bot \) AD' nên B'C \( \bot \) AD'
Vậy ta đã chứng minh được rằng tứ diện ACB'D' có các cặp cạnh đối diện vuông góc với nhau.