Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

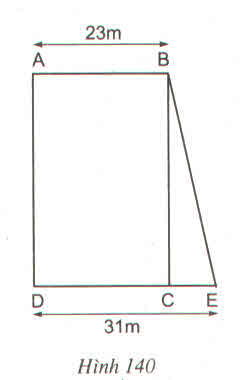
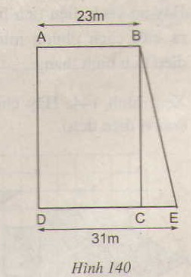
Ta có SABCD = AB. AD = 828 m2
Nêm AD = 8282382823 = 36 (m)
Do đó diện tích của hình thang ABED là:
SABED= (AB+DE).AD2(AB+DE).AD2 = (23+31).362(23+31).362 = 972(m2)

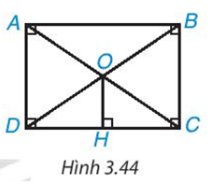
Xét tam giác DBC, ta có:
O là trung điểm cạnh BD (tính chất hình chữ nhật)
OH // BC (cùng vuông góc với CD)
⇒ OH là đường trung bình tam giác BCD.
⇒ H là trung điểm của CD (đpcm).

tam giácABC : MN là đường trung bình => MN// AC ,tam giác ADC có DP là đường trung bình => QP//AC ==> MN//QP(1) Xét r=tam giác BCD có NP là đường trung binh=> NP//BD=> GÓC MNP=90 ĐỘ(2) từ 1 và 2 => MNPQ là hình chữ nhật b) MNPQ/ABCD=1/2 C) diện tích ABCD=9.6/2=27 , diện tích MNPQ=27/2=13.5 diện tích MNB=3.375

`a)`
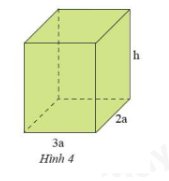
Biểu thức biểu thị V của hình HCN là:
`3a*2a*h = 6a^2 * h` `(cm^3)`
Biểu thức biểu thị S xung quanh của HCN là:
`(3a+2a)*2*h = 5a*2*h = 10a*h` `(cm^2)`
`b)`
Thay `a = 2` cm; `h = 5` cm
V của hình HCN đó là:
`6*2^2 * 5 = 24 * 5 =120 (cm^3)`
S xung quanh của hình HCN đó là:
`10*2*5 = 10*10 = 100 (cm^2)`
Vậy: `a) 6a^2 * h`; `10a*h`
`b) 120` `cm^3;` `100` `cm^2.`
`a,` Thể tích: `V = h . 2a . 3a = 6a^2h`.
Diện tích xung quanh: `S_(xq) = (3ah+2ah) xx 2 = 10ah`.
`b, V = 6 . 2^2 . 5 = 120 cm^2`
`S = 10 . 2 . 5 = 100 cm^2`

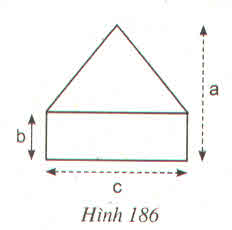
Ta có hình thang ABCD ( AB// CD), với đường trung bình EF và hình chữ nhật GHIK như hình vẽ .
Dễ dàng chứng minh
∆AEG = ∆DEK;
∆BFH = ∆CFI
Do đó SABCD = SAEKIFB + SDEK + SCFI = SAEKIFB + SAEG + SBFH = SGHIK
Nên
SABCD = SGHIK = EF. AJ mà EF = EF=AB+CD2EF=AB+CD2
Do đó SABCD = SABCD=AB+CD2.AJSABCD=AB+CD2.AJ
Vậy ta gặp lại công thức tính diện tích hình thang đã được học nhưng bằng một phương pháp chứng minh khác. Mặt khác, ta phát hiện công thức mới : Diện tích hình thang bằng tích của đường trung bình hình thang với chiều cao.

Ta có hình thang ABCD ( AB// CD), với đường trung bình EF và hình chữ nhật GHIK như hình vẽ .
Dễ dàng chứng minh
∆AEG = ∆DEK;
∆BFH = ∆CFI
Do đó SABCD = SAEKIFB + SDEK + SCFI = SAEKIFB + SAEG + SBFH = SGHIK
Nên
SABCD = SGHIK = EF. AJ mà EF = EF=AB+CD2EF=AB+CD2
Do đó SABCD = SABCD=AB+CD2.AJSABCD=AB+CD2.AJ
Vậy ta gặp lại công thức tính diện tích hình thang đã được học nhưng bằng một phương pháp chứng minh khác. Mặt khác, ta phát hiện công thức mới : Diện tích hình thang bằng tích của đường trung bình hình thang với chiều cao.
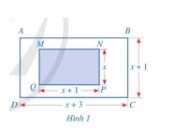

Biểu thức diện tích của hình chữ nhật ABCD là: \({S_{ABC{\rm{D}}}} = \left( {x + 1} \right)\left( {x + 3} \right)\)
Biểu thức diện tích của hình chữ nhật MNPQ là: \({S_{MNPQ}} = x\left( {x + 1} \right)\)
Tỉ số diện tích của hình chữ nhật ABCD và hình chữ nhật MNPQ là: \(\dfrac{{{S_{ABC{\rm{D}}}}}}{{{S_{MNPQ}}}} = \dfrac{{\left( {x + 1} \right)\left( {x + 3} \right)}}{{x\left( {x + 1} \right)}} = \dfrac{{x + 3}}{x}\)
b) Với x = 5 ta có: \(\dfrac{{{S_{ABC{\rm{D}}}}}}{{{S_{MNPQ}}}} = \dfrac{{5 + 3}}{5} = \dfrac{8}{5}\)
Với x = 2 ta có: \(\dfrac{{{S_{ABC{\rm{D}}}}}}{{{S_{MNPQ}}}} = \dfrac{{2 + 3}}{2} = \dfrac{5}{2}\)