Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Lấy điểm X trên tia đối của tia BC sao cho BX=DE, suy ra tam giác ABX bằng tam giác ADE (cạnh huyền, cạnh góc vuông). Do đó AX=AE. Xét tam giác vuông XAF, áp dụng hệ thức liên hệ giữa cạnh góc vuông và đường cao ta có \(\frac{1}{AX^2}+\frac{1}{AF^2}=\frac{1}{AB^2}\to\frac{1}{AE^2}+\frac{1}{AF^2}=\frac{1}{AB^2}\) không đổi.
b. Kẻ EH vuông góc với KF. Ta có \(\sin EKF\cdot\cos EFK+\sin EFK\cdot\cos EKF=\frac{EH\cdot FH}{KE\cdot EF}+\frac{KH\cdot EH}{KE\cdot EF}=\frac{EH\left(FH+KH\right)}{KE\cdot EF}=\frac{EH\cdot KF}{KE\cdot EF}\)
\(\frac{2S_{KEF}}{KE\cdot EF}=\frac{KA\cdot EF}{KE\cdot EF}=\frac{KA}{KE}=\sin\angle AEK=\cos\angle AKE.\) (ĐPCM)
cho hình thoi ABCD có canh .Qua C vẽ đường thẳng M cắt các tia đối của các tia BA và DA theo thứ tự E và F.CMR tổng 1/AE +1/AF không đổi với mọi vị trí nói trên cảu đường thẳng m
BÁC NÀO BK CHỈ MK VS

Lời giải:
Áp dụng hệ thức lượng trong tam giác vuông với tam giác $ADC$:
$\frac{1}{DE^2}=\frac{1}{AD^2}+\frac{1}{DC^2}=\frac{1}{6^2}+\frac{1}{8^2}$
$\Rightarrow DE=4,8$ (cm)
Áp dụng hệ thức lượng trong tgv với tam giác $ADF$:
$AD^2=DE.DF$
$6^2=4,8.DF\Rightarrow DF=7,5$ (cm)
$EF=DF-DE=7,5-4,8=2,7$ (cm)
Tiếp tục áp dụng hệ thức lượng trong tgv $ADF$:
$AE^2=DE.DF=4,8.2,7=12,96\Rightarrow AE=3,6$ (cm)
$AF=\sqrt{AE^2+EF^2}=\sqrt{3,6^2+2,7^2}=4,5$ (cm) theo định lý Pitago
$BF=AB-AF=CD-AF=8-4,5=3,5$ (cm)
Áp dụng htl trong tgv với tam giác $ADC$:
$DE^2=AE.CE$
$4,8^2=3,6.CE\Rightarrow CE=6,4$ (cm)

A B C D F E G
a) * Xét \(\Delta ADF\) và \(\Delta ABE\) có \(\left\{{}\begin{matrix}AE=AF\\AD=AB\\FAD=EAB\end{matrix}\right.\)
\(\Rightarrow\) \(\Delta ADF=\Delta ABE\left(c.g.c\right)\) \(\Rightarrow ADF=ABE\) . Mà \(ABE=90^0\) \(\Rightarrow ADF=90^0\)
* Có \(ADF+ADC=90^0+90^0=180^0\) \(\Rightarrow\) F , D , C thẳng hàng _ đpcm
b) Xét \(\Delta AFG\) vuông tại A có đường cao AD \(\Rightarrow\dfrac{1}{AD^2}=\dfrac{1}{AF^2}+\dfrac{1}{AG^2}\)
Mà AD=AB ; AF=AE
\(\Rightarrow\dfrac{1}{AB^2}=\dfrac{1}{AE^2}+\dfrac{1}{AG^2}\) _đpcm

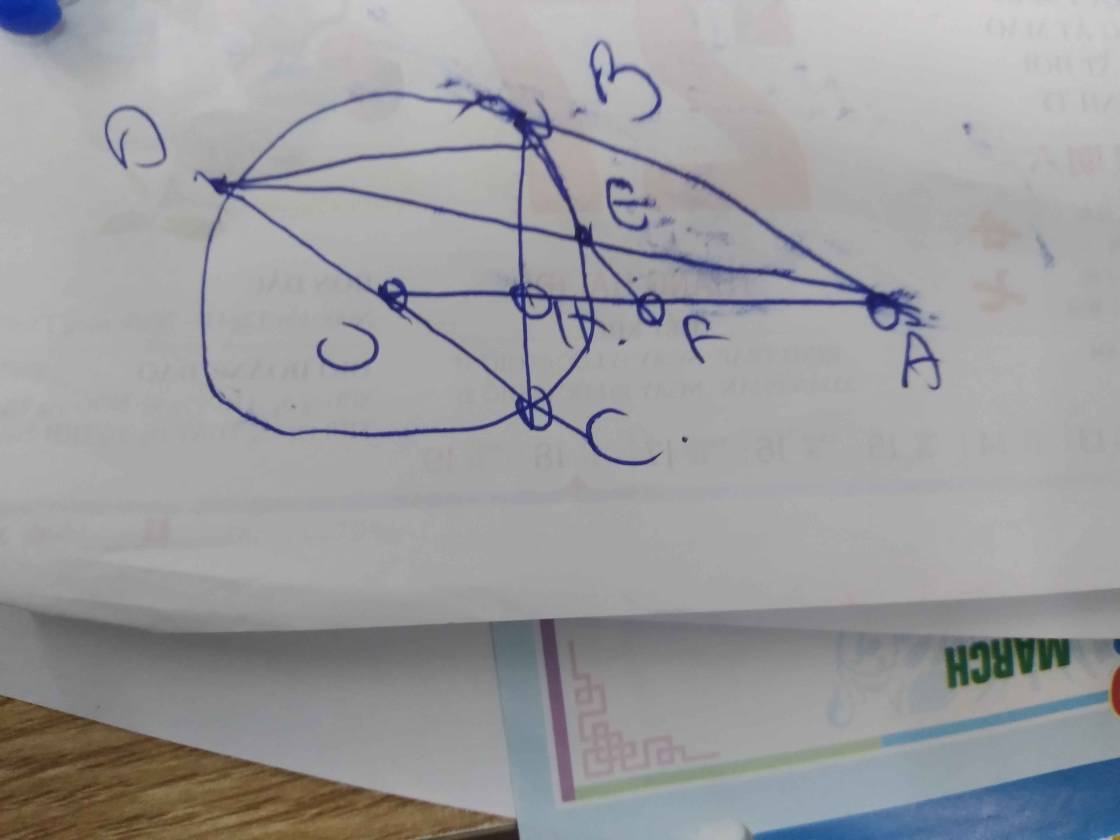
Đường tròn c: Đường tròn qua B_1 với tâm O Đoạn thẳng i: Đoạn thẳng [F, A] Đoạn thẳng k: Đoạn thẳng [A, C] Đoạn thẳng l: Đoạn thẳng [A, E] Đoạn thẳng m: Đoạn thẳng [E, M] Đoạn thẳng n: Đoạn thẳng [D, F] Đoạn thẳng p: Đoạn thẳng [G, B] Đoạn thẳng q: Đoạn thẳng [E, C] O = (2.08, 1.84) O = (2.08, 1.84) O = (2.08, 1.84) A = (12.48, 2.58) A = (12.48, 2.58) A = (12.48, 2.58) Điểm B: Điểm trên c Điểm B: Điểm trên c Điểm B: Điểm trên c Điểm D: Điểm trên c Điểm D: Điểm trên c Điểm D: Điểm trên c Điểm C: Giao điểm đường của c, f Điểm C: Giao điểm đường của c, f Điểm C: Giao điểm đường của c, f Điểm E: Giao điểm đường của c, g Điểm E: Giao điểm đường của c, g Điểm E: Giao điểm đường của c, g Điểm F: Giao điểm đường của c, h Điểm F: Giao điểm đường của c, h Điểm F: Giao điểm đường của c, h Điểm G: Giao điểm đường của c, i Điểm G: Giao điểm đường của c, i Điểm G: Giao điểm đường của c, i Điểm M: Giao điểm đường của f, j Điểm M: Giao điểm đường của f, j Điểm M: Giao điểm đường của f, j
a) Do DF // AC nên \(\widehat{MAG}=\widehat{GFD}\) (Hai góc so le trong) .
Lại có \(\widehat{GFD}=\widehat{GED}\) (Hai góc nội tiếp cùng chắn cung GD)
Nên \(\widehat{MAG}=\widehat{GED}\)
Xét tam giác AMG và tam giác EMA có:
\(\widehat{MAG}=\widehat{MEA}\) (cmt)
Góc M chung
Vậy nên \(\Delta AMG\sim\Delta EMA\left(g-g\right)\Rightarrow\frac{MA}{ME}=\frac{MG}{MA}\Rightarrow MA^2=MG.ME\)
b) Do tứ giác ECBG nội tiếp nên \(\widehat{BCE}=\widehat{BGM}\) (Góc ngoài tại đỉnh đối của tứ giác nội tiếp)
Vậy xét tam giác MGB và MCE có:
\(\widehat{BGM}=\widehat{ECM}\left(cmt\right)\)
Góc M chung
Vậy nên \(\Delta MGB\sim\Delta MCE\left(g-g\right)\)
c) Theo câu a, ta có \(AM^2=MG.ME\)
Theo câu b, \(\Delta MGB\sim\Delta MCE\Rightarrow\frac{MG}{MC}=\frac{MB}{ME}\Rightarrow MG.ME=MB.MC\)
Vậy nên \(MA^2=MB.MC\)
Suy ra \(MA^2+MA.MC=MB.MC+MA.MC\)
\(\Leftrightarrow MA\left(MA+MC\right)=MC\left(MB+MA\right)\)
\(\Leftrightarrow MA.AC=MC.AB\)
\(\Leftrightarrow AB\left(AC-AM\right)=MA.AC\)
\(\Leftrightarrow AB.AC-AB.AM=AM.AC\)
\(\Leftrightarrow AB.AC=AM\left(AB+AC\right)\)
\(\Leftrightarrow\frac{1}{AM}=\frac{AB+AC}{AB.AC}\)
\(\Leftrightarrow\frac{1}{AM}=\frac{1}{AB}+\frac{1}{AC}\left(đpcm\right)\)