Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi O là giao điểm của hai đường chéo AC và BD.
AC = BD (tính chất hình chữ nhật)
\(\Rightarrow OA=OD=\dfrac{1}{2}AC\)
\(AD=\dfrac{1}{2}AC\left(gt\right)\)
\(\Rightarrow OA=OD=AD\)
\(\Rightarrow\Delta OAD\) đều
\(\Rightarrow\widehat{AOD}=60^0\)

Xét tam giác vuông ACD vuông tại A có AD=AC/2 => ACD=30 độ => ADC=60 độ
Gọi giao điểm 2 đường chéo của hcn là O => OA=OD => tam giác AOD cân tại O mà ADC = 60 độ => tam giác AOD đều => AOD=60 độ :)


Cách dựng:
- Dựng ∆ OAB biết OA = OB = 2cm
\(\widehat{AOB}=100^o\)
- Trên tia đối tia OA dựng điểm C sao cho OC = OA = 2cm
- Trên tia đối tia OB dựng điểm D sao cho OD = OB = 2cm
Nối AD, BC, CD ta có hình chữ nhật ABCD cần dựng.

Tia AB cắt DC tại E.
=> AC là tia phân giác của \(\widehat{DAE}\left(gt\right)\)
\(\Rightarrow AC\perp DE\left(gt\right)\)
=> Tam giác ADE cân.
Lại có: \(\widehat{D}=60^o\Rightarrow\Delta ADE\) là tam giác đều.
=> C là trung điểm DE (AC đồng thời la trung tuyến)
Mà: BC//AD => BC là đường trung bình của \(\Delta ADE\)
Ta có: \(AB=DC=\frac{AD}{2},BC=\frac{AD}{2}\)
Giả thiết: \(AB+BC+CD+AD=20\)
\(\Rightarrow\frac{AD}{2}+\frac{AD}{2}+\frac{AD}{2}+AD=20\)
\(\Rightarrow\frac{5}{2}AD=20\Rightarrow AD=8\left(cm\right)\)

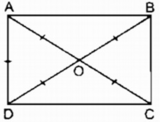
Gọi O là giao điểm của hai đường chéo AC và BD.
Ta có: AC = BD ( tính chất hình chữ nhật) ⇒ OA = OD = 1/2 AC
Lại có: AD = 1/2 AC (gt)
Suy ra: OA = OD = AD
⇒ ∆ OAD đều ⇒ ∠ (AOD ) = 60 0

O A B C D
Gọi giao điểm của hai đường chéo là \(O\) .
Theo bài ra thì \(\widehat{AOD}=30^o\)
Theo tính chât hình chữ nhật thì \(OA=OD\) ( cùng bằng nửa độ dài đường chéo )
\(\Rightarrow\Delta OAD\) cân tại O
\(\Rightarrow\widehat{CAD}=\widehat{OAD}=\frac{180^o-\widehat{AOD}}{2}=\frac{180^o-30^o}{2}=75^o\)
Xét tam giác vuông tại D là DAC :
\(\frac{AD}{AC}=cos\widehat{CAD}\Rightarrow AD=cos\widehat{CAD}.AC=cos75^o.4\)
\(\frac{DC}{AC}=sin\widehat{CAD}\Rightarrow DC=ACsin\widehat{CAD}=4sin75^o\)
Do đó diện tích ABCD là :
\(AD.DC=4cos75^o.4sin75^o=4\left(cm^2\right)\)

Hình vẽ ;
A D B C E 60 o
a, Chứng minh tứ giác ABCD là hình thang cân .
Xét tam giác ADC ( góc ACD = 90 độ do AC\(⊥\)CD-gt) ta có :
\(\widehat{D}+\widehat{CAD}=90^o\)
\(\Rightarrow\widehat{CAD}=90^o-\widehat{D}=90^o-60^o=30^o\)
mà \(\widehat{CAD}=\widehat{BAC}\left(gt\right)\Rightarrow\widehat{BAC}=30^o\)
Ta có : \(\widehat{BAD}=\widehat{BAC}+\widehat{CAD}=30^o+30^o=60^o\)
Xét hình thang ABCD , ta có :
\(\widehat{BAD}=\widehat{D}=60^o\)
\(\Rightarrow\)tứ giác ABCD là hình thang cân.
b, Tính AD.
Kéo dài AB và DC cắt nhau tại E .
Xét tam giác AED , ta có : \(\widehat{BAC}=\widehat{CAD}\left(gt\right)\)
\(AC⊥CD\)(gt)
=> tam giác AED là tam giác cân .
mà góc D = 60 độ (gt)
=> tam giác AED là tam giác đều
=>\(\hept{\begin{cases}AB=CD=\frac{1}{2}AD\left(1\right)\\CE=CD\end{cases}}\)
Xét tam giác ADE , ta có :
BC//AD( do ABCD là hình thang )
CE=CD( cmt)
=> BC là đường trung bình của tam giác ADE
=>\(BC=\frac{1}{2}AD\left(2\right)\)
Từ (1) và (2) => BC=CD=AB=\(\frac{1}{2}.AD\)
Theo giả thiết , ta có :
AB+BC+CD+AD=20
=>\(\frac{1}{2}AD+\frac{1}{2}AD+\frac{1}{2}AD+AD=20\)
=>\(\frac{5}{2}AD=20\Rightarrow AD=8\left(cm\right)\)
Nên nhớ hình vẽ chỉ mang tính minh họa cho bài làm nên ko được đẹp lắm đâu các bạn thông cảm cho.
Trong bài mk làm hơi tắt có j hk hiểu nhắn tin hỏi mk .
Chọn C