Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) áp dụng vào định lý pi ta go ta có
BD^2=AB^2+AD^2
BD^2=4^2+3^2
BD^2=25
BD=5

$#Shả$
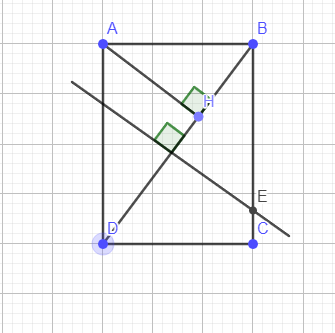
`a)` Xét `\triangleAHB` và `\triangleBCD` ta có `:`
`\hat{AHB}=\hat{BCD}=90^{o}`
`\hat{ABH}=\hat{BDC} ` (slt)
Vậy `\triangleAHB ` $\backsim$ `\triangleBCD` (g-g)
a) △AHB và △BCD có: \(\widehat{AHB}=\widehat{BCD}=90^0\); \(\widehat{ABH}=\widehat{BDC}\) (AB//DC).
\(\Rightarrow\)△AHB∼△BCD (g-g).
b) △ABD có: \(BD^2=AD^2+AB^2\Rightarrow BD=\sqrt{AD^2+AB^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
△AHB∼△BCD \(\Rightarrow\dfrac{AH}{BC}=\dfrac{AB}{BD}=\dfrac{HB}{CD}\)
\(\Rightarrow\left[{}\begin{matrix}AH=\dfrac{AB.BC}{BD}=\dfrac{3.4}{5}=2,4\left(cm\right)\\HB=\dfrac{AB.CD}{BD}=\dfrac{3.3}{5}=1,8\left(cm\right)\end{matrix}\right.\)
\(\Rightarrow S_{AHB}=\dfrac{1}{2}AH.HB=\dfrac{1}{2}.2,4.1,8=2,16\left(cm^2\right)\)
c) ABCD là hình chữ nhật, AC cắt BD tại O.
\(\Rightarrow\)O là trung điểm của AC và BD.
BD⊥DE tại D, CF⊥DE tại F. \(\Rightarrow\)BD//CF.
-△ODE có: IF//OD \(\Rightarrow\dfrac{IF}{OD}=\dfrac{EI}{EO}\).
-△OBE có: IC//OB \(\Rightarrow\dfrac{IC}{OB}=\dfrac{EI}{EO}=\dfrac{IF}{OD}\Rightarrow IC=IF\Rightarrow\)I là trung điểm CF.

Bạn tự vẽ hình nha.
a) Xét hai tam giác BDC và EDB có:
\(\widehat{BDC}\left(\widehat{EDB}\right)\): góc chung
\(\widehat{BCD}=\widehat{EBD}\)= 900
Vậy \(\Delta\)BDC ~ \(\Delta\)EDB
\(\Rightarrow\dfrac{DB}{DE}=\dfrac{DC}{DB}\Rightarrow DB^2=DC.DE\)
b) Vì tam giác ABC vuông tại A
⇒ BD2 = AB2 + AD2
= 32 + 42
= 52
⇒BD = 5cm.
Ta có:
BC2 = CD. CE
\(\Rightarrow CE=\dfrac{BC^2}{CD}=\dfrac{9}{4}=2,25\)(cm)
c) Ta có BD // CF ( ⊥ BE)
\(\Rightarrow\dfrac{IC}{OD}=\dfrac{IE}{OE}\) và \(\dfrac{IF}{OB}=\dfrac{IE}{OE}\)
\(\Rightarrow\dfrac{IC}{OD}=\dfrac{IF}{OB}\Rightarrow IC=IF\)( vì O là giao điểm hai đường chéo của HCN nên OB = OD)
Vậy I là trung điểm của đoạn CF. (đpcm)
d) Vì BD // CF nên BDCF là hình thang.
O và I lần lượt là trung điểm 2 cạnh đáy của BDCF.
E là giao điểm của hai cạnh bên BF và CD, OE đi qua hai trung điểm của hai cạnh đáy nên OE phải đi qua giao điểm của hai đường chéo của hình thang BDCF.
Mà OE cắt BC tại K nên đường chéo DF phải đi qua K.
Vậy ba điểm D, K, F thẳng hàng. (đpcm)

a: XétΔBDC vuông tại C và ΔEDB vuông tại B có
góc BDC chung
Do đo:ΔBDC đồng dạng với ΔEDB
Suy ra: DB/DE=DC/DB
hay \(DB^2=DE\cdot DC\)
b: \(BD=\sqrt{3^2+4^2}=5\left(cm\right)\)
\(CE=\dfrac{CB^2}{CD}=\dfrac{3^2}{4}=2.25\left(cm\right)\)

a: BD=5cm
b: Xég ΔBCD vuông tại C và ΔCFB vuông tại F có
góc BDC=góc CBF
Do đó:ΔBCD đồng dạg với ΔCFB
Suy ra: BC/CF=BD/CB
=>3/CF=5/3
=>CF=1,8(cm)