Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

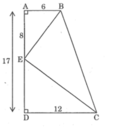
Ta có: AD = AE + DE
Suy ra: DE = AD – AE = 17 – 8 = 9cm
Xét △ ABE và △ DEC, ta có:
∠ A = ∠ D = 90 0 (1)
Mà :
Suy ra: 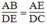 (2)
(2)
Từ (1) và (2) suy ra : △ ABE đồng dạng △ DEC (c.g.c)
Suy ra: ∠ ABE = ∠ DEC
Trong △ ABE ta có: ∠ A = 90 0 ⇒ ∠ (AEB) + ∠ (ABE) = 90 0
Suy ra: ∠ (AEB) + ∠ (DEC) = 90 0
Lại có: ∠ (AEB) + ∠ (BEC) + ∠ (DEC) = 180 0 (kề bù)
Vậy : ∠ (BEC) = 180 0 - ( ∠ (AEB) + ∠ (DEC)) = 180 0 - 90 0 = 90 0

ta có:
SABC = SADC
SAFE = SAHE
SEKC = SEGC
=> SABC – SAFE – SEKC = SADC – SAHE - SEGC
hay SEFBK = SEGDH

Tương tự bài 2A ta có S M B C D N = S A B C D − S A M N = 60 − 1 2 ( 10 − x ) . ( 6 − x )
\(S_{ABCD}=AB.AD=48\Rightarrow S_{BCDE}=30\)
\(S_{BCDE}=\dfrac{1}{2}CD.\left(ED+BC\right)=\dfrac{1}{2}.6.\left(8-x+8\right)=30\)
\(\Rightarrow x=6\)