Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
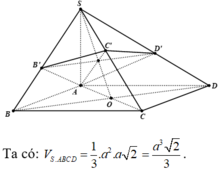
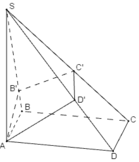
Dựa vào giả thiết ta có B', C', D' lần lượt là hình chiếu của A lên SB, SC, SD.
Tam giác SAC vuông cân tại A nên C' là trung điểm của SC.
Trong tam giác vuông SAB' ta có:
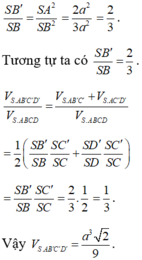


\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABCD)
\(\Rightarrow\widehat{SBA}=45^0\Rightarrow\Delta SAB\) vuông cân \(\Rightarrow\left\{{}\begin{matrix}SA=AB=a\\SB=a\sqrt{2}\end{matrix}\right.\)
\(SC=\sqrt{SA^2+AC^2}=\sqrt{a^2+2a^2}=a\sqrt{3}\)
\(\dfrac{V_{SAHIK}}{V_{SABCD}}=\dfrac{2V_{SAHI}}{2V_{SABC}}=\dfrac{V_{SAHI}}{V_{SABC}}=\dfrac{SH}{SB}.\dfrac{SI}{SC}=\left(\dfrac{SA}{SB}\right)^2\left(\dfrac{SA}{SC}\right)^2=\left(\dfrac{a}{a\sqrt{2}}\right)^2\left(\dfrac{a}{a\sqrt{3}}\right)^2=\dfrac{1}{6}\)
\(\Rightarrow V_{SAIHK}=\dfrac{1}{6}V_{SABCD}=\dfrac{1}{6}.\dfrac{1}{3}.SA.AB^2=\dfrac{a^3}{18}\)
Bạn coi lại đề, AHIK là 1 tứ giác nên ko thể có thể tích

Chọn C.
Dễ thấy BD ⊥ SC, nên BD // (AB'C'D'), suy ra BD // B'D'.
Gọi I = AC ∩ BD, J = AC' ∩ SI, khi đó J là trọng tâm của tam giác SAC và J ∈ B'D'.
Suy ra
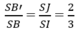
Do đó dễ thấy
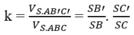

Chắc là mp (P) đi qua A'
Đặt \(V_{SABCD}=V\)
Theo định lý Talet: \(\dfrac{SA'}{SA}=\dfrac{SB'}{SB}=\dfrac{SC'}{SC}=\dfrac{SD'}{SD}=\dfrac{3}{4}\)
Ta có: \(\dfrac{V_{SA'B'C'D'}}{V_{SABCD}}=\dfrac{2V_{SA'B'C'}}{2V_{SABC}}=\dfrac{V_{SA'B'C'}}{V_{SABC}}=\dfrac{SA'}{SA}.\dfrac{SB'}{SB}.\dfrac{SC'}{SC}=\dfrac{3}{4}.\dfrac{3}{4}.\dfrac{3}{4}=\dfrac{27}{64}\)
Tỉ số thể tích 2 phần (phần trên chia phần dưới) là: \(\dfrac{27}{64}:\left(1-\dfrac{27}{64}\right)=\dfrac{27}{37}\)



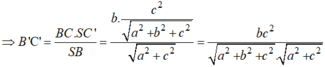
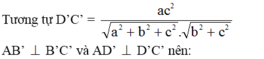 S
∆
A
B
'
C
'
=
1
2
B
'
C
'
.
A
B
'
=
1
2
.
c
2
a
2
+
c
2
.
b
a
2
+
b
2
+
c
2
.
c
a
a
2
+
c
2
S
∆
A
B
'
C
'
=
1
2
B
'
C
'
.
A
B
'
=
1
2
.
c
2
a
2
+
c
2
.
b
a
2
+
b
2
+
c
2
.
c
a
a
2
+
c
2
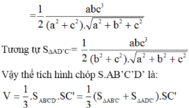
![]()
![]()
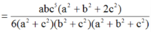
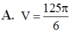
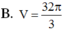
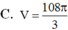
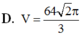

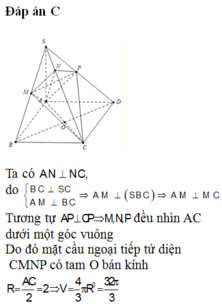
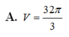
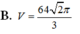


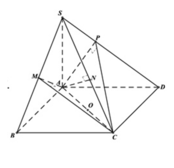
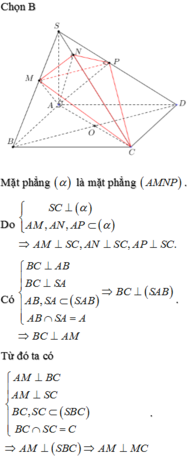


Do \(SA=SB=SC=SD\) và đáy là hình vuông nên \(SABCD\) là chóp đều
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
Theo tính đối xứng của chóp đều \(\Rightarrow SB'=SD'\Rightarrow B'D'||BD\)
Gọi M là giao điểm SO và AC' \(\Rightarrow M\in B'D'\) (t/c giao tuyến 3 mp cắt nhau)
Áp dụng định lý Talet:
\(\dfrac{SM}{SO}=\dfrac{SD'}{SD}=\dfrac{SB'}{SB}=\dfrac{2}{3}\Rightarrow M\) là trọng tâm tam giác SAC
\(\Rightarrow C'\) là trung điểm SC \(\Rightarrow\dfrac{SC'}{SC}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{V_{SAB'C'D'}}{V_{SABCD}}=\dfrac{2V_{SAB'C'}}{2V_{SABC}}=\dfrac{V_{SAB'C'}}{V_{SABC}}=\dfrac{SA}{SA}.\dfrac{SB'}{SB}.\dfrac{SC'}{SC}=1.\dfrac{2}{3}.\dfrac{1}{2}=\dfrac{1}{3}\)