Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:$ABCD$ là hình vuông nên $AC=\sqrt{2}a$
Ta thấy: $SA^2+SC^2=a^2+a^2=2a^2=AC^2$
$\Rightarrow SAC$ là tam giác vuông tại $S$
$\Rightarrow \overrightarrow{SA}.\overrightarrow{SC}=0$

\(BD=a\sqrt{2}\)
\(\widehat{\left(\overrightarrow{BD};\overrightarrow{BS}\right)}=\widehat{SBD}=\dfrac{SB^2+BD^2-SD^2}{2SB.BD}=\dfrac{a^2+2a^2-a^2}{2a.a\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{\left(\overrightarrow{BD};\overrightarrow{BS}\right)}=45^0\)
thầy ơi bưa trước thầy em có giảng cái cách mà SB=SD thì suy ra SBD là nửa hình vuông nên góc SBD 45 độ v đúng ko thầy?

Đáp án D

Gọi O = AC ∩ BD
Vì ABCD là hình thoi nên AC ⊥ BD tại O.
Tam giác SBD cân tại S nên SO ⊥ BD.
Suy ra BD
⊥
(SAC)![]()
Do ![]() => SO = OC
=> SO = OC![]()
![]()
![]()
![]()
![]()
![]()
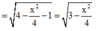
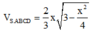
Đặt 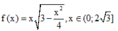
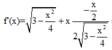
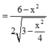
![]()
Bảng biến thiên:
| x |
0 |
|
|
+ 0 - |
|
|
|
Vậy ![]()

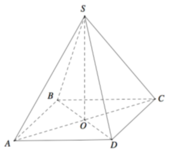
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{SAO}\) hay \(\widehat{SAC}\) là góc giữa SA và (ABCD)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(cos\widehat{SAC}=\dfrac{SA^2+AC^2-SC^2}{2SA.AC}=\dfrac{\sqrt{2}}{2}\)

Tứ giác ABCD là hình vuông nên A C = A B 2 + B C 2 = a 2 + a 2 = a 2
Tam giác SAC có SA = a, SC = a và AC = a√2 ⇒ SAC là tam giác vuông tại S, hay SA ⊥ SC
Đáp án A
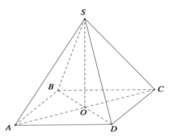
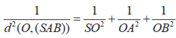
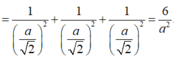
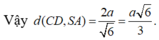



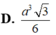


\(\overrightarrow{SA}.\overrightarrow{CD}=\overrightarrow{SA}.\overrightarrow{BA}=\overrightarrow{AS}.\overrightarrow{AB}=a.a.cos60^0=\dfrac{a^2}{2}\)