Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
=>SB vuông góc AC
mà AC vuông góc BD
nên AC vuông góc (SBD)
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=>BD vuông góc SA
b: Xét ΔACB có CO/CA=CI/CB
nên OI//AB
=>OI vuông góc BC
BC vuông góc OI
BC vuông góc SO
=>BC vuông góc (SOI)
=>(SBC) vuông góc (SOI)

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AM\) (1)
Tam giác SAB vuông cân tại A (do SA=SB=a)
\(\Rightarrow AM\perp SB\) (trung tuyến đồng thời là đường cao) (2)
(1);(2)\(\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM\perp SC\)
Hoàn toàn tương tự ta có \(AN\perp SC\)
\(\Rightarrow SC\perp\left(AMN\right)\Rightarrow\left(SAC\right)\perp\left(AMN\right)\)
Từ A kẻ \(AH\perp SC\Rightarrow H\in\left(AMN\right)\)
Lại có \(SA\perp\left(ABCD\right)\Rightarrow\left(SAC\right)\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{HAC}\) là góc giữa (AMN) và (ABCD)
\(AC=a\sqrt{2}\) ; \(SC=a\sqrt{3}\)
\(sin\widehat{HAC}=cos\widehat{SCA}=\dfrac{AC}{SC}=\sqrt{\dfrac{2}{3}}\Rightarrow\widehat{HAC}\approx54^044'\)

.png)
+ SA⊥(ABCD)⇒SA⊥BDSA⊥(ABCD)⇒SA⊥BD (1)
+ ABCD là hình vuông ⇒AC⊥BD⇒AC⊥BD (2)
+ Từ (1) và (2) suy ra BD⊥(SAC)⇒BD⊥SCBD⊥(SAC)⇒BD⊥SC

Câu hỏi của Phạm Thùy Dương - Toán lớp 11 - Học toán với OnlineMath
Em tham khảo bài làm tại link này nhé!
Cộng đồng học tập online | Học trực tuyến
Lần sau các bài Toán lớp 10, 11, 12 các em đăng trong trang Cộng đồng học tập online | Học trực tuyến nhé! olm hầu như để giải đáp thắc mắc của HỌc sinh tiểu học và trung học em nhé :). Chúc em học tập tốt :)<3

Có : AC vuông góc với BD (hình vuông ABCD)
SA vuông góc với BD ( do SA vuông góc với mp ABCD)
=> BD vuông góc với mp SAC...

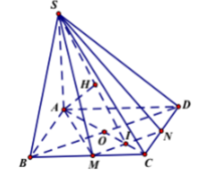
AM là hình chiếu của SM trên (ABCD).
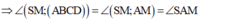
- Xét tam giác vuông ABM ta có: 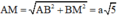
- Xét tam giác vuông SAM ta có: 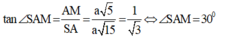


Dựng CH _|_ AB => CH _|_ (SAB)
Giả sử MN cắt AD tại F. Theo định lý Talet ta có:
\(\frac{DF}{MC}=\frac{ND}{NC}=\frac{1}{2}\Rightarrow DF=\frac{MC}{2}=\frac{a}{4}\)
Khi đó \(\frac{PA}{PC}=\frac{AF}{MC}=\frac{5}{2}\Rightarrow\frac{CA}{PA}=\frac{7}{5}\)
Do đó: d (P;(SAB))=\(\frac{5}{7}d\left(C;\left(SAB\right)\right)=\frac{5}{7}CH=\frac{5}{7}\cdot\frac{a\sqrt{3}}{2}=\frac{5a\sqrt{3}}{14}\)

Gọi H là trung điểm AO \(\Rightarrow HM\) là đường trung bình tam giác SAO
\(\Rightarrow\left\{{}\begin{matrix}HM//SO\\HM=\frac{1}{2}SO\end{matrix}\right.\) \(\Rightarrow HM\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{MNH}\) là góc giữa MN và (ABCD) \(\Rightarrow\widehat{MNH}=60^0\)
\(NH=\sqrt{\left(\frac{3a}{4}\right)^2+\left(\frac{a}{4}\right)^2}=\frac{a\sqrt{10}}{4}\)
\(\Rightarrow MH=NH.tan60^0=\frac{a\sqrt{30}}{4}\)
\(SO=2MH=\frac{a\sqrt{30}}{2}\)
\(MN=\frac{NH}{cos60^0}=\frac{a\sqrt{10}}{2}\)
b/ Gọi E; F lần lượt là trung điểm AB; AD \(\Rightarrow EF//BD\) \(\Rightarrow\left(MEF\right)//\left(SCD\right)\Rightarrow\) góc giữa MN và (SBD) bằng góc giữa MN và (MEF)
\(EN//AC\) (do EN là đường trung bình tam giác ABC)
Mà \(AC\perp\left(SBD\right)\Rightarrow AC\perp\left(MEF\right)\Rightarrow EN\perp\left(MEF\right)\)
\(\Rightarrow\widehat{NME}\) là góc giữa NM và (MEF)
\(EN=\frac{AC}{2}=\frac{a\sqrt{2}}{2}\)
\(\Rightarrow sin\widehat{NME}=\frac{EN}{MN}=\frac{\sqrt{5}}{5}\Rightarrow\widehat{NME}\approx26^033'\)