Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề; SA=SB=SC=SD=2a
SA=SB
OA=OB
=>SO là trung trực của AB
=>SO vuông góc AB(2)
SA=SD
OA=OD
=>SO là trung trực của AD
=>SO vuông góc AD(1)
Từ (1), (2) suy ra SO vuông góc (ABCD)
(SC;(ABCD))=(CS;CO)=góc SCO
\(OC=\dfrac{a\sqrt{2}}{2}\)
\(SO=\sqrt{SA^2+AO^2}\)
\(=\sqrt{\left(2a\right)^2+\left(\dfrac{a\sqrt{2}}{2}\right)^2}=\sqrt{4a^2+\dfrac{1}{2}a^2}=\dfrac{3}{\sqrt{2}}a\)
\(SC=\sqrt{SO^2+OC^2}=\sqrt{\dfrac{9}{2}a^2+\dfrac{1}{2}a^2}=a\sqrt{5}\)
\(cosSCO=\dfrac{OC}{SC}\)
\(=\dfrac{a\sqrt{2}}{2}:a\sqrt{5}=\dfrac{\sqrt{2}}{2\sqrt{5}}\)
=>\(\widehat{SCO}\simeq72^0\)
=>\(\left(SC;\left(ABCD\right)\right)=72^0\)

Em kiểm tra lại đề, \(\left(\alpha\right)\) đi qua AI nên nó không thể cắt SA tại M được nữa (vì nó đi qua A nên đã cắt SA tại A rồi)

Đề bài \(\Rightarrow SA\perp\left(ABCD\right)\)
\(3\overrightarrow{SM}=\overrightarrow{SB}+2\overrightarrow{SC}=\overrightarrow{SM}+\overrightarrow{MB}+2\overrightarrow{SM}+2\overrightarrow{MC}\)
\(\Leftrightarrow\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}\Rightarrow M\) là điểm nằm giữa BC đồng thời \(MB=2MC\Rightarrow\left\{{}\begin{matrix}MB=2\\MC=1\end{matrix}\right.\)
Tương tự, N nằm giữa CD sao cho \(NC=2\) ; \(ND=1\)
Qua N kẻ đường thẳng song song DM cắt AB kéo dài tại P
Tới đây thì vấn đề đơn giản: quy về tìm khoảng các giữa A và (SNP).
Kéo dài DM cắt AB kéo dài tại E, Talet: \(\dfrac{CD}{AE}=\dfrac{CM}{BM}=\dfrac{1}{2}\Rightarrow AE=2CD=6\)
Nối AN cắt DM tại F, Talet: \(\dfrac{NF}{AF}=\dfrac{DN}{AE}=\dfrac{1}{6}\Rightarrow\dfrac{NF}{AN}=\dfrac{1}{7}\)
\(\Rightarrow d\left(DM;SN\right)=d\left(DM;\left(SNP\right)\right)=d\left(F;\left(SNP\right)\right)=\dfrac{1}{7}d\left(A;\left(SNP\right)\right)\)
Tứ giác DNPE là hbh \(\Rightarrow DN=EP=1\Rightarrow AP=7\)
Tính k/c từ A đến (SNP) bạn tự hoàn thành nhé, rất cơ bản
Bài này nếu được áp dụng tọa độ của 12 thì rất lẹ
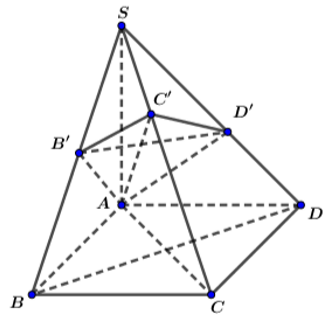





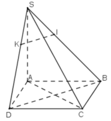



\(BD=a\sqrt{2}\)
\(\widehat{\left(\overrightarrow{BD};\overrightarrow{BS}\right)}=\widehat{SBD}=\dfrac{SB^2+BD^2-SD^2}{2SB.BD}=\dfrac{a^2+2a^2-a^2}{2a.a\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{\left(\overrightarrow{BD};\overrightarrow{BS}\right)}=45^0\)
thầy ơi bưa trước thầy em có giảng cái cách mà SB=SD thì suy ra SBD là nửa hình vuông nên góc SBD 45 độ v đúng ko thầy?