Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: SO vuông góc (ABC)
=>(SGO) vuông góc (ABC)
b: ((SAB);(ABC))=(SG;AG)=góc SGA
\(AG=\dfrac{a\sqrt{3}}{3}\)
cos SGA=AG/SA=căn 3/3:2=căn 3/6
=>góc SGA=73 độ

a: \(\widehat{SB;AB}=\widehat{SBA}\)
SA\(\perp\)(ABC)
=>\(SA\perp AB;SA\perp AC;SA\perp BC\)
Xét ΔSAB vuông tại A có \(tanSBA=\dfrac{SA}{AB}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
=>\(\widehat{SBA}=60^0\)
=>\(\widehat{SB;AB}=60^0\)
b:
\(\widehat{SC;AC}=\widehat{SCA}\)
Xét ΔSAC vuông tại A có \(tanSCA=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
nên \(\widehat{SCA}=60^0\)
=>\(\widehat{SC;AC}=60^0\)
c: ΔABC đều có AM là đường trung tuyến
nên \(AM=BC\cdot\dfrac{\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\)
Ta có: SA\(\perp\)(ABC)
AM\(\subset\)(ABC)
Do đó: SA\(\perp\)AM
=>ΔSAM vuông tại A
\(\widehat{SM;AM}=\widehat{SMA}\)
Xét ΔSMA vuông tại A có \(tanSMA=\dfrac{SA}{AM}=\dfrac{a\sqrt{3}}{\dfrac{a\sqrt{3}}{2}}=2\)
=>\(\widehat{SMA}\simeq63^026'\)
=>\(\widehat{SM;AM}\simeq63^026'\)
a.
Góc giữa SB và AB là góc \(\widehat{SBA}\)
Trong tam giác vuông SAB:
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
\(\Rightarrow\widehat{SBA}=60^0\)
b.
Góc giữa SC và AC là góc \(\widehat{SCA}\)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=\sqrt{3}\Rightarrow\widehat{SCA}=60^0\)
c.
Góc giữa SM và AM là góc \(\widehat{SMA}\)
AM là trung tuyến tam giác đều \(\Rightarrow AM=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow tan\widehat{SMA}=\dfrac{AM}{SA}=2\Rightarrow\widehat{SMA}=60^026'\)

Ta tính côsin của góc giữa hai vectơ S C → và A B → . Ta có
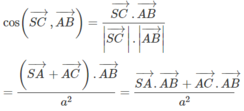
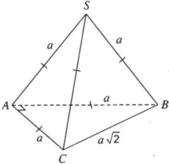
Theo giả thiết ta suy ra hình chóp có các tam giác đều là SAB, SAC và các tam giác vuông là ABC vuông tại A và SBC vuông tại S.
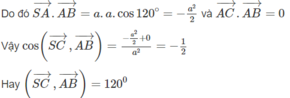
Vậy góc giữa hai vectơ A B → v à S C → bằng 120 o .

Dựng hình vuông ABDC
\(\Rightarrow SA=SB=SC=SD=2\) ; \(CD=AB=2\)
\(CD||AB\Rightarrow\widehat{\left(AB;SC\right)}=\widehat{\left(CD;SC\right)}=\widehat{SCD}\)
Tam giác SCD có \(SC=SD=CD\Rightarrow\Delta SCD\) đều
\(\Rightarrow\widehat{SCD}=60^0\)

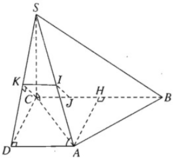
a) Gọi H là trung điểm của đoạn BC. Qua A vẽ AD song song với BC và bằng đoạn HC thì góc giữa BC và SA là góc ∠SAD. Theo định lí ba đường vuông góc, ta có SD ⊥ DA và khi đó:
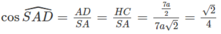
Vậy góc giữa BC và SA được xác định sao cho 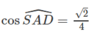
Vì BC // AD nên BC song song với mặt phẳng (SAD). Do đó khoảng cách giữa SA và BC chính là khoảng cách từ đường thẳng BC đến mặt phẳng (SAD).
Ta kẻ CK ⊥ SD, suy ra CK ⊥ (SAD), do đó CK chính là khoảng cách nói trên. Xét tam giác vuông SCD với đường cao CK xuất phát từ đỉnh góc vuông C ta có hệ thức:

Chú ý. Nếu kẻ KI // AD và kẻ IJ // CK thì IJ là đoạn vuông góc chung của SA và BC.

a.
Do \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp SB\)
b.
\(SA\perp\left(ABC\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABC)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABC)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)




ông này khuya rồi đăng bài nhiều d :(((
vẫn hình vẽ ấy lập luận tương tự
Gọi M là trung điểm của AB ta có:
AB _|_ SM ( tam giác SAB cân tại S ) (1)
AB _|_ CM ( tam giác ABC đều ) (2)
Từ (1),(2) suy ra AB vuông góc SCM
suy ra góc (AB,SC)=90