Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TenAnh1 TenAnh1 A = (-0.14, -7.4) A = (-0.14, -7.4) A = (-0.14, -7.4) B = (14.46, -7.36) B = (14.46, -7.36) B = (14.46, -7.36) C = (-3.74, -5.6) C = (-3.74, -5.6) C = (-3.74, -5.6) D = (11.62, -5.6) D = (11.62, -5.6) D = (11.62, -5.6) E = (-3.34, -5.86) E = (-3.34, -5.86) E = (-3.34, -5.86) F = (12.02, -5.86) F = (12.02, -5.86) F = (12.02, -5.86) G = (-3.7, -5.88) G = (-3.7, -5.88) G = (-3.7, -5.88) H = (11.66, -5.88) H = (11.66, -5.88) H = (11.66, -5.88) I = (-3.74, -5.62) I = (-3.74, -5.62) I = (-3.74, -5.62) J = (11.62, -5.62) J = (11.62, -5.62) J = (11.62, -5.62) A'

S A B C I H O K
a) \(SB^2=AS^2+AB^2=AS^2+AC^2=SC^2\Rightarrow SB=SC\) => \(\Delta\)SBC cân tại S
Do đó: AO,SH cắt nhau tại trung điểm I của cạnh BC
Xét \(\Delta\)SBC: trực tâm H, đường cao SI => \(IH.IS=IB.IC\)(1)
Tương tự: \(IB.IC=IO.IA\)(2)
Từ (1);(2) => \(IH.IS=IO.IA\)=> \(\Delta\)IHO ~ \(\Delta\)IAS => ^IHO = ^IAS = 900 => OH vuông góc IS (3)
Ta có: BC vuông góc với AI,AS => BC vuông góc với (SAI) => BC vuông góc OH (4)
Từ (3);(4) => OH vuông góc (SBC).
b) Xét tam giác SKI: IO vuông góc SK tại A, KO vuông góc SI tại H (cmt) => O là trực tâm tam giác SKI
Vậy SO vuông góc IK.

Do (SAB) và (SAC) vuông góc với đáy (ABC)
Và (ABC) ∩ (SAC) = SA nên SA ⊥ (ABC)
BC ⊥ AH, BC ⊥ SA
⇒ BC ⊥ ((SAH)
Mà BC ⊂ (SBC) nên (SAH) ⊥ (SBC)

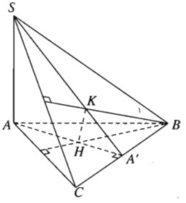
a) Gọi A’ là giao điểm của AH và BC. Ta cần chứng minh ba điểm S, K, A’ thẳng hàng.
Vì H là trực tâm của tam giác ABC nên AA′ ⊥ BC. Mặt khác theo giả thiết ta có: SA ⊥ (ABC), do đó SA ⊥ BC.
Từ đó ta suy ra BC ⊥ (SAA′) và BC ⊥ SA′. Vậy SA’ là đường cao của tam giác SBC nên SA’ là phải đi qua trực tâm K. Vậy ba đường thẳng AH, SK và BC đồng quy.
b) Vì K là trực tâm của tam giác SBC nên BK ⊥ SC (1)
Mặt khác ta có BH ⊥ AC vì H là trực tâm của tam giác ABC và BH ⊥ SA vì SA ⊥ (ABC).
Do đó BH ⊥ (ABC) nên BH ⊥ SC (2).
Từ (1) và (2) ta suy ra SC ⊥ (BHK). Vì mặt phẳng (SAC) chứa SC mà SC ⊥ (BHK) nên ta có (SAC) ⊥ (BHK).
c) Ta có
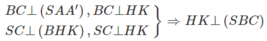
Mặt phẳng (BHK) chứa HK mà HK ⊥ (SBC) nên (BHK) ⊥ (SBC).

S A B C H K
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAC\right)\)
\(\Rightarrow BC\perp AH\) (1)
Mà \(AH\perp SC\) (2)
(1);(2) \(\Rightarrow AH\perp\left(SBC\right)\)
\(\frac{SH}{SC}=\frac{SK}{SB}\Rightarrow HK//BC\) (định lý Talet đảo)
\(\Rightarrow HK\perp\left(SAC\right)\) (do \(BC\perp\left(SAC\right)\)
\(\Rightarrow HK\perp SA\)
\(HK\perp\left(SAC\right)\Rightarrow HK\perp SC\) (3)
(2);(3) \(\Rightarrow SC\perp\left(AHK\right)\Rightarrow SC\perp AK\)
\(AH\perp\left(SBC\right)\) (cmt) \(\Rightarrow\) BH là hình chiếu vuông góc của AB lên (SBC)
\(\Rightarrow\widehat{ABH}\) là góc giữa AB và (SBC)
\(\frac{1}{AH^2}=\frac{1}{SA^2}+\frac{1}{AC^2}=\frac{1}{a^2}+\frac{1}{a^2}=\frac{2}{a^2}\Rightarrow AH=\frac{a\sqrt{2}}{2}\)
\(AB=\sqrt{AC^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow sin\widehat{ABH}=\frac{AH}{AB}=\frac{1}{2}\Rightarrow\widehat{ABH}=30^0\)


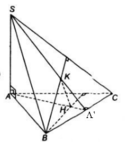




a. Chắc bạn ghi nhầm đề, AH và AK cắt nhau tại A trong khi BC ko đi qua A nên 3 đường này ko thể đồng quy
b. Ta có: \(CH\perp AB\) (do H là trực tâm)
\(SA\perp CH\) (do SA vuông góc mặt đáy)
\(\Rightarrow CH\perp\left(SAB\right)\Rightarrow\left(SAB\right)\perp\left(CHK\right)\)
Do \(CH\perp\left(SAB\right)\Rightarrow CH\perp SB\)
Mà \(SB\perp CK\) (K là trực tâm SBC)
\(\Rightarrow SB\perp\left(CHK\right)\Rightarrow\left(SBC\right)\perp\left(CHK\right)\)
c/ Gọi M là giao điểm AH với BC
\(\Rightarrow BC\perp\left(SAM\right)\Rightarrow\left(SBC\right)\perp\left(SAM\right)\)
Mà \(\left(SAM\right)\cap\left(CHK\right)=HK\)
\(\Rightarrow HK\perp\left(SBC\right)\)
giúp em bài hinh hoc voi anh anh giỏi hình mà