Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có (SBD) giao với (ABCD) theo gt BD
BD vuông AC và BD vuong SA nên BD vuông (SAC)
góc đó là góc SOA
xét tam giác vuông SAO có tan 60*=SA/ÁO mà AC= a căn 2 nên ÁO=a căn 2 trên 2
=>SA=a căn 6 trên 2
xét VSABCD =SB.SC =1/2.1/2=1/4 (M,N là trung diểm)
VSAMND SM.SN
MÀ VSABCD=1/3.SA.SABCD=1/3.a căn 6/2.a^2=a^3 căn 6/6
=>VSAMND=1/4.VSABCD=a căn 6/24

\(V=\dfrac{1}{3}SA.S_{ABCD}\Rightarrow S_{ABCD}=\dfrac{3V}{SA}=22\sqrt{3}\)
\(\Rightarrow\dfrac{1}{2}AB.AD+\dfrac{1}{2}BC.CD=22\sqrt{3}\)
\(\Leftrightarrow5AD+3CD=44\) (1)
Mặt khác: \(\left\{{}\begin{matrix}BD^2=AB^2+AD^2=AD^2+75\\BD^2=BC^2+CD^2=CD^2+27\end{matrix}\right.\)
\(\Rightarrow AD^2+75=CD^2+27\Rightarrow AD^2+48=CD^2\) (2)
Giải hệ (1) và (2) ta được \(\left\{{}\begin{matrix}AD=4\\CD=8\end{matrix}\right.\)
Từ A kẻ \(AH\perp BD\) \(\Rightarrow BD\perp\left(SAH\right)\) \(\Rightarrow\left(SBD\right)\) và (ABCD) đều vuông góc (SAH)
\(\Rightarrow\widehat{SHA}\) là góc giữa (SBD) và đáy
Hệ thức lượng tam giác vuông ABD:
\(\dfrac{1}{AH^2}=\dfrac{1}{AD^2}+\dfrac{1}{AB^2}=\dfrac{91}{1200}\Rightarrow AH=\dfrac{20\sqrt{273}}{91}\)
\(cot\widehat{SHA}=\dfrac{AH}{SA}=\dfrac{20\sqrt{273}}{819}\)
gọi x là độ dài cạnh AD; y là độ dài cạnh CD
\(\Rightarrow S_{ABCD}=S_{BAD}+S_{BCD}=\dfrac{1}{2}.AB.AD+\dfrac{1}{2}BC.CD=\dfrac{1}{2}5\sqrt{3}x+\dfrac{1}{2}3\sqrt{3}y\)
\(\Rightarrow V_{SABCD}=\dfrac{1}{3}SA.S_{ABCD}=\dfrac{1}{3}.9.\left(\dfrac{1}{2}.5\sqrt[]{3}x+\dfrac{1}{2}3\sqrt{3}y\right)=\dfrac{3\sqrt{3}}{2}\left(5x+3y\right)=66\sqrt{3}\\ \Rightarrow5x+3y=44\)
\(AH\perp BD\left(H\in BD\right)\\ cot\left(\left(SBD\right),\left(ABCD\right)\right)=\widehat{SHA}\Rightarrow cot\widehat{SHA}=\dfrac{SA}{AH}\)


\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SMA}\) là góc giữa SM và đáy
\(\Rightarrow\widehat{SMA}=60^0\Rightarrow SA=AM.tan60^0=\sqrt{3a^2+\left(\dfrac{2a}{2}\right)^2}.\sqrt{3}=2a\sqrt{3}\)
Qua B kẻ đường thẳng song song AM cắt AD kéo dài tại E
\(\Rightarrow AM||\left(SBE\right)\Rightarrow d\left(AM;SB\right)=d\left(AM;\left(SBE\right)\right)=d\left(A;\left(SBE\right)\right)\)
Từ A kẻ \(AH\perp BE\) , từ A kẻ \(AK\perp SH\Rightarrow AK=d\left(A;\left(SBE\right)\right)\)
\(\widehat{DAM}=\widehat{AEB}\) (đồng vị) , mà \(\widehat{BAH}=\widehat{AEB}\) (cùng phụ \(\widehat{ABH}\))
\(\Rightarrow\widehat{DAM}=\widehat{BAH}\)
\(\Rightarrow AH=AB.cos\widehat{BAH}=AB.cos\widehat{DAM}=\dfrac{AB.AD}{AM}=\dfrac{2a.a\sqrt{3}}{2a}=a\sqrt{3}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}=\dfrac{1}{3a^2}+\dfrac{1}{12a^2}=\dfrac{5}{12a^2}\)
\(\Rightarrow AK=\dfrac{2a\sqrt{15}}{5}\)

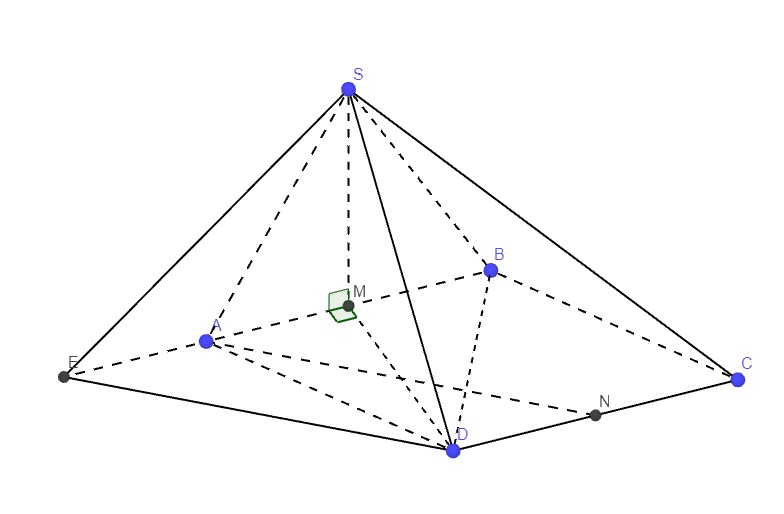
Gọi E là điểm đối xứng M qua A
\(\Rightarrow ANDE\) là hình bình hành (cặp cạnh đối AE và DN song song và bằng nhau)
\(\Rightarrow AN||DE\Rightarrow\) góc giữa AN và SD bằng góc giữa SD và DE
Do tam giác ABD đều \(\Rightarrow MD\perp AB\) \(\Rightarrow\Delta MDE\) vuông tại M
Do tam giác SAB đều \(\Rightarrow SM\perp AB\)
Mà \(\left(SAB\right)\perp\left(ABCD\right)\Rightarrow SM\perp\left(ABCD\right)\)
\(\Rightarrow\) Các tam giác SMD, SME vuông tại M
\(SM=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác SAB đều)
\(MD=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác ABD đều)
\(ME=2AM=AB=a\)
Pitago:
\(SD=\sqrt{SM^2+MD^2}=\dfrac{a\sqrt{6}}{2}\)
\(SE=\sqrt{SM^2+ME^2}=\dfrac{a\sqrt{7}}{2}\)
\(ED=\sqrt{MD^2+ME^2}=\dfrac{a\sqrt{7}}{2}\)
\(\Rightarrow cos\widehat{SDE}=\dfrac{SD^2+ED^2-SE^2}{2SD.ED}=\dfrac{\sqrt{42}}{14}\)

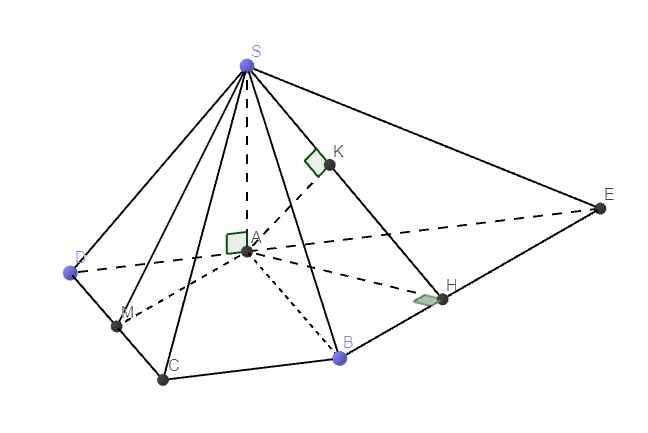
Gọi H là hình chiếu vuông góc của S lên đáy \(\Rightarrow\) H là tâm đáy
Gọi E là trung điểm BH \(\Rightarrow ME\perp BD\Rightarrow ME\perp\left(SBD\right)\)
\(\Rightarrow\widehat{MSE}=30^0\)
Ta có: \(ME=\dfrac{1}{2}CH\) (đường trung bình) \(=\dfrac{1}{4}AC=\dfrac{a\sqrt{2}}{4}\)
\(\Rightarrow SM=\dfrac{ME}{sin30^0}=\dfrac{a\sqrt{2}}{2}\) ; \(HM=\dfrac{1}{2}AB=\dfrac{a}{2}\)
\(\Rightarrow SH=\sqrt{SM^2-HM^2}=\dfrac{a}{2}\)
\(V=\dfrac{1}{3}SH.AB^2=\dfrac{a^3}{6}\)