Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sxq=1/2*40*13=20*13=260cm2
Độ dài cạnh ở đáy là 40/4=10cm
V=10^2*12=1200cm3

Sxq=16*4*17/2=544cm2
Stp=544+16^2=800cm2
V=1/3*16^2*15=1280cm3
Nữa chu vi đáy của hình chóp đều:
\(16\cdot4:2=32\left(cm\right)\)
Diện tích xung quanh của hình chóp đều:
\(S_{xq}=32\cdot17=544\left(cm^2\right)\)
Diện tích mặt đáy của hình chóp đều:
\(S_đ=16^2=256\left(cm^2\right)\)
Diện tích toàn phần của hình chóp đều:
\(S_{tp}=S_đ+S_{xq}=544+256=800\left(cm^2\right)\)
Thể tích của hình chóp đều:
\(V=\dfrac{1}{3}\cdot256\cdot15=1280\left(cm^3\right)\)

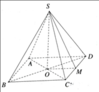
Xét hình chóp cụt đều ABCD.AB'C'D'
Gọi M ,M' thứ tự là trung điểm của BC , B'C' . Khi đó MM' là đường cao của hình thang cân BCC'B' . Do đó diện tích xung quanh của hình chóp cụt đều là :
\(S_{xq}=4.\dfrac{a+b}{2}.MM'=\left(2a+2b\right).MM'\)
Từ giả thiết , ta có :
\(\left(2a+2b\right).MM'=a^2+b^2hayMM'=\dfrac{a^2+b^2}{2\left(a+b\right)}\left(1\right)\)
Dễ thấy OM // O'M' nên OM và O'M' xác định mặt phẳng (OMM'O') . Trong mặt phẳng (OMM'O') , kẻ MH \(\perp\) O'M' . Khi đó : \(HM'=O'M'-O'H=\dfrac{b-a}{2}\)
Trong tam giác vuông MHM' ta có :
\(MM'^2=MH^2+HM'^2=h^2+\left(\dfrac{b-a}{2}\right)^2\left(2\right)\)
Từ (1) và (2) suy ra :
\(h^2+\left(\dfrac{b-a}{2}\right)^2=\dfrac{\left(a^2+b^2\right)^2}{4\left(a+b\right)^2}\)
\(\Rightarrow h^2=\dfrac{\left(a^2+b^2\right)^2-\left(b^2-a^2\right)^2}{4\left(a+b\right)^2}=\dfrac{a^2b^2}{\left(a+b\right)^2}\)
Vậy \(h=\dfrac{ab}{a+b}\)

Gọi \(a\) là cạnh đáy hình chóp tứ giác đều \(\left(cm\right)\)
\(h\) là chiều cao hình chóp tứ giác đều \(\left(cm\right)\)
\(d\) là trung đoạn\(\left(cm\right)\)
Ta có :
\(S_{xq}=4S=4.\dfrac{1}{2}a.d=2ad\)
mà \(d^2=h^2+\dfrac{a^2}{4}\Rightarrow d=\sqrt[]{h^2+\dfrac{a^2}{4}}\)
\(\Rightarrow S_{xq}=2a\sqrt[]{h^2+\dfrac{a^2}{4}}\)
\(\Leftrightarrow S^2_{xq}=4a^2\left(h^2+\dfrac{a^2}{4}\right)=4a^2h^2+a^4\)
\(\Leftrightarrow a^4+4a^2h^2-S^2_{xq}=0\)
\(\Leftrightarrow a^4+4a^2.36-36^2=0\)
\(\Leftrightarrow a^4+144a^2-1296=0\left(1\right)\)
\(\Delta'=5184+1296=6480\Rightarrow\sqrt[]{\Delta'}=36\sqrt[]{5}\)
Pt (1) có nghiệm \(a^2=-72+36\sqrt[]{5}=36\left(1-\sqrt[]{5}\right)\)
\(\)\(\Rightarrow a=6\sqrt[]{1-\sqrt[]{5}}\left(cm\right)\) (cạnh đáy là hình vuông)
Vậy cạnh đáy tứ giác đều là \(a=6\sqrt[]{1-\sqrt[]{5}}\left(cm\right)\)
Đính chính
\(...a^2=-72+36\sqrt[]{2}=36\left(\sqrt[]{5}-2\right)\)
\(\Rightarrow a=6\sqrt[]{\sqrt[]{5}-2}\left(cm\right)\)
Vậy cạnh tứ giác đều là \(a=6\sqrt[]{\sqrt[]{5}-2}\left(cm\right)\)


Thể tích là:
\(V=\dfrac{1}{3}\cdot36\cdot9=12\cdot9=108\left(cm^3\right)\)