Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
+ Hình nón có chiều cao h và bán kính R thì có thể tích là
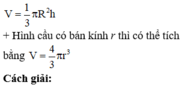
Vì hình nón có bán kính R và chiều cao h bằng nhau nên h = R và thể tích hình nón đã cho là

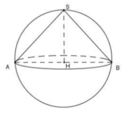
Khi đó H là tâm đường tròn ngoại tiếp tam giác SAB và H cũng là tâm mặt cầu ngoại tiếp hình nón đỉnh S.
Nên bán kính mặt cầu là HS = R nên thể tích hình cầu này
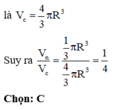

Đáp án A.
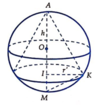
Kí hiệu như hình vẽ.
Ta thấy I K = r ' là bán kính đáy của hình chóp, A I = h là chiều cao của hình chóp.
Tam giác vuông tại K có IK là đường cao
⇒ I K 2 = A I . I M ⇒ r ' 2 = h . 2 r − h
Ta có V c o h p = 1 3 . π r ' 2 . h = 1 3 . π . h . h . 2 r − h = 4 3 π . h 2 . h 2 2 r − h .
Áp dụng bất đẳng thức Cauchy ta có
h 2 . h 2 . 2 r − h ≤ h 2 + h 2 + 2 r − h 3 27 = 8 r 3 27
⇔ V c h o p ≤ 4 3 π . 8 r 3 27 = 32 81 . π r 3
Dấu bằng xảy ra khi h 2 = 2 r − h ⇔ h = 4 r 3 . Vậy ta chọn A

Đáp án B
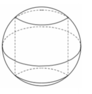
Gọi chiều cao và bán kính đáy của hình trụ nội tiếp mặt cầu lần lượt là h, r
Ta có tâm mặt cầu là trung tâm của đường nối 2 tâm các đường tròn đáy của hình trụ
Khi đó, bán kính mặt cầu ngoại tiếp khối trụ là R 2 = r 2 + h 2 4
Thể tích khối trụ là V = πr 2 h = π 4 4 R 2 - h 2 . h
Theo bất đẳng thức Cosi cho 3 số nguyên dương, ta có
4 R 2 - h 2 4 R 2 - h 2 2 h 2 ≤ 4 R 2 - h 2 + 4 R 2 - h 2 + 2 h 2 3 27
Nên 4 R 2 - h 2 . h 2 ≤ 256 R 6 27 ⇒ V ≤ π 4 4 R 2 - h 2 h ≤ 4 π 3 9 R 3
Dấu bằng xảy ra khi và chỉ khi 4 R 2 - h 2 = 2 h 2 ⇔ h = 2 R 3 3 .

Gọi ST là đường sinh hình nón
Ta có:
tan I S T ^ = 3 3 ⇒ O S T ^ = I S T ^ = 30 o
∆ O I T c ó R = O T cos 30 o = 3 2 . 2 3 = 1
Vậy V = 4 3 πR 3 = 4 π 3
Đáp án C

Đáp án A
Theo bài ra, ta có khối nón (N) nội tiếp khối cầu (S).
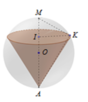
Giả sử khối nón (N) có đỉnh A, tâm đáy I như hình vẽ bên với h = I A là chiều cao và bán kính đáy r = I K
Tam giác AMK vuông tại K, có I K 2 = I A . I M ⇔ r 2 = h 2 R − h
Suy ra V N = 1 3 π r 2 h = π 3 h 2 2 R − h = π 3 . 2 R h 2 − h 3
Xét hàm số f h = 2 R h 2 − h 3 trên khoảng 0 ; 2 R → max f h = 32 R 3 27
Vậy thể tích cần tính là V = π 3 . 32 R 3 27 = 32 π R 3 81
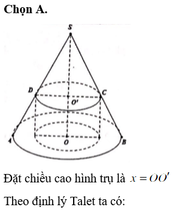

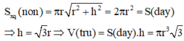


Đáp án A.
Gọi R là bán kính của hình cầu (S). Bài toán có thể quy về: “Cho đường tròn tâm O, bán kính R ngoại tiếp hình vuông ABCD và nội tiếp ∆ S E F đều” (hình vẽ).
Hình vuông ABCD nội tiếp đường tròn (O) nên
A B = B D = 2 R = A B 2 ⇔ A B = 2 R .
⇒ Bán kính đáy và chiều cao của hình trụ (T) lần lượt là r = A B 2 = 2 R 2 và h = A B = 2 R .
Thể tích khối trụ là V T = πr 2 h = π . 2 R 2 2 . 2 R = π 2 R 3 2 .
Ta có ∆ S E F đều và ngoại tiếp đường tròn (O) nên O là trọng tâm của Δ S E F .
Gọi H là trung điểm của EF thì S H = 3 O H = 3 R ⇒ H F = S H . tan 30 ° = R 3
⇒ Bán kính đáy và chiều cao của hình nón (N) lần lượt là H F = R 3 và S H = 3 R . Thể tích khối nón là V N = 1 3 π . HF 2 . SH = 1 3 π R 3 2 . 3 R = 3 πR 3 .
Vậy V T V N = π 2 R 3 2 3 πR 3 = 2 6 .