Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E F G H I K N M Q P
a) - Xét tứ giác AMCI , có :
+ AM // CI ( GT )
+ AM = CI ( GT )
=> AMCI là hình bình hành ( 2 cạnh đối song song và bằng nhau )
=> AI // MC hay EH // FG (1)
- XÉt tứ giác BNDK có :
+ BN // DK ( GT )
+ BN = DK ( GT : N , K lần lượt là trung điểm BC , DA và BC = DA )
=> BNDK là hình bình hành ( 2 cạnh đối song song và bằng nhau )
=> BK // DN hay EF // HG ( 2)
- Từ 1 và 2 ta có : EFGH là hình bình hành ( các cặp cạnh đối song song )
- Kẻ FQ vuông góc AI tai Q
=> \(S_{EFGH\:}=FQ.EH\)
- Mặt khác : \(S_{AMCI}=FQ.AI\)( Vì MC // AI nên FQ là đường cao chung )
=> \(\frac{S_{EFGH\:}}{S_{AMCI}}=\frac{FQ.EH}{FQ.AI}=\frac{EH}{AI}\)(3)
- LẠi có :
+ Xét tam giác AHD có : KE // DH và K là trung điểm của AD nên => E là trung điểm của AH hay AE = EH
+ Xét tam giác DCG có : HI // CG , I là trung điểm của DC nên => H là trung diểm của DG => HI là đường trung bình của tam giác DCG => \(HI=\frac{1}{2}.CG\)mà CG = FG = EH nên \(HI=\frac{1}{2}.EH\)
=> \(AI=AE+EH+HI=2.EH+\frac{1}{2}.EH=\frac{5.EH}{2}\)
Thay vào 3 , ta được :
\(\frac{S_{EFGH\:}}{S_{AMCI}}=\frac{EH}{AI}=EH:\frac{5.EH}{2}=\frac{2.EH}{5.EH}=\frac{2}{5}\)
b) - Kẻ AP vuông góc với CD tại Q
- Ta có : \(S_{ABCD}=AP.CD\)và \(S_{AMCI}=AP.CI\)
=> \(\frac{S_{AMCI}}{S_{ABCD}}=\frac{AP.CI}{AP.CD}=\frac{CI}{CD}=\frac{1}{2}\Rightarrow S_{AMCI}=\frac{1}{2}.S_{ABCD}\)
Từ ý a , ta có : \(S_{EFGH\:}=\frac{2}{5}.SAMCI=\frac{2}{5}.\frac{1}{2}.S_{ABCD}=\frac{1}{5}.S_{ABCD}\)
MÀ ABCD có diện tích là S nên \(S_{EFGH\:}=\frac{1}{5}.S\)

a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Suy ra: AF//CE

a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Suy ra: AF//CE

1:
Xet ΔOAE và ΔOCF có
góc OAE=góc OCF
góc AOE=góc COF
=>ΔOAE đồng dạng với ΔOCF
=>AE/CF=OE/OF
Xét ΔOEB và ΔOFD có
góc OEB=góc OFD
góc EOB=góc FOD
=>ΔOEB đồng dạng với ΔOFD
=>EB/FD=OE/OF=AE/CF
mà CF=DF
nên EB=AE
=>E là trung điểm của BA

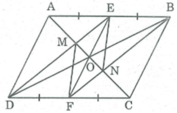
Xét ∆ EOM và ∆ FON có: ∠ (MEO) = ∠ (NFO) (so le trong do DE//BF)
OE = OF (tính chất hình bình hành)
∠ (MOE)= ∠ (NOF) (đối đỉnh )
Suy ra: ∆ EOM = ∆ FON (g.c.g) ⇒ OM = ON
Vậy tứ giác EMFN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường).

đầu bài chỗ " đường chéo BD cắt AE" chắc là " đường chéo BD cắt AI" phải không bn???
a) ta có: AB = CD ( ABCD là h.b.h)
=> AK = IC \(\left(=\frac{1}{2}AB=\frac{1}{2}CD\right)\)
mà AK // IC
=> AKCI là hình bình hành ( dấu hiệu)
xét \(\Delta DFC\)
có: DI =IC (gt)
EI // FC ( AKCI là h.b.h)
=> EI là đường trung bình của \(\Delta DFC\)
=> DE = EF ( t/c')
cmtt với \(\Delta AEB\)ta có: EF = FB
=> DE=EF=FB
b) xét \(\Delta ABD\)
có: AM=MD
AK=KB
=> KM là đường trung bình của \(\Delta ABD\)
=> KM // BD và \(KM=\frac{1}{2}BD\)
cmtt với \(\Delta BCD\)ta có: IN//BD và \(IN=\frac{1}{2}BD\)
=> KM // IN (//BD)
\(KM=IN\left(=\frac{1}{2}BD\right)\)
=> KMIN là hình bình hành ( dấu hiệu)