Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này có gì đâu em ! Anh làm nhé !
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE

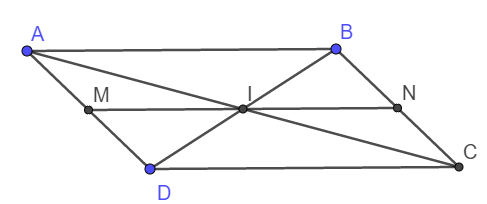
1. Xét tam giác ABD có MI // AB nên theo định lý Talet ta có:
\(\frac{MI}{AB}=\frac{DI}{DB}\)
Xét tam giác ABC có NI // AB nên theo định lý Talet ta có:
\(\frac{NI}{AB}=\frac{NC}{BC}\)
2. Xét tam giác BDC có IN // DC nên \(\frac{DI}{DB}=\frac{NC}{BC}\)
Từ đó ta có: \(\frac{MI}{AB}=\frac{NI}{AB}\Rightarrow MI=IN\)
Vậy I là trung điểm MN (đpcm)

A B C D E F M N P G
Tứ giác ABCD là hình bình hành => AB//CD; AD//BC.
=> Giao điểm của AC; BD là trung điểm của mỗi đường
=> N là trung điểm BD (1)
Ta có: AE//BD. Mà AD//BE => Tứ giác AEBD là hình bình hành.
=> 2 đường chéo DE và AB cắt nhau tại trung điểm của mỗi đường.
=> M là trung điểm AB (2)
Tương tự: Tứ giác ABDF là hình bình hành
=> P là trung điểm AD (3)
Từ (1); (2) và (3) => G là trọng tâm của tam giác BAD.
=> AN, DM, BP đồng quy = >AC; DE; BF đồng quy (điều cần c/m).