Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác BMDN có
BM//DN
BM=DN
Do đó: BMDN là hình bình hành
b: AM+MB=AB
CN+ND=CD
mà MB=ND và AB=CD
nên AM=CN
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
c: AMCN là hình bình hành
=>AN//CM
=>NK//MH
BMDN là hình bình hành
=>BN//DM
=>NH//KM
Xét tứ giác MKNH có
MK//NH
MH//NK
Do đó: MKNH là hình bình hành

a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
b: ABCDlà hình bình hành
nên AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm của AC
AMCN là hình bình hành
nên AC cắt MN tại trung điểm của mỗi đường
=>M đối xứng N qua O

1.a) Ta có : góc MAN= GÓC MCN \(\Rightarrow\)NC // AM (1)
Lại có ABCD là hình bình hành \(\Rightarrow\) AB//=DC (2)
từ (1) và (2) \(\Rightarrow\) ANCM là hình bình hành( tứ giác có 2 cặp cạnh // với nhau)
2)
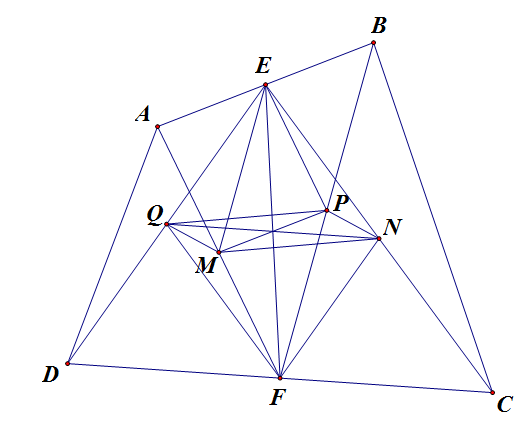
Sử dụng tính chất đường trung bình. Dễ dàng chứng minh QENF,MEPFQENF,MEPF là hình bình hành
Vậy EFEF và QNQN giao nhau tại trung điểm mỗi đường, EFEF và MPMP giao nhau tại trung điểm mỗi đường.
⇒QN⇒QN giao MPMP tại trung điểm mỗi đường.
Vậy QPNMQPNM là hình bình hành.
Xét tam giác ADM và tam giác CBN có:
AD = CN (ABCD là hình bình hành)
ADM = CBN (2 góc so le trong, AB // CB)
DM = BN (gt)
=> Tam giác ADM = Tam giác CBN (c.g.c)
=> AM = CN (2 cạnh tương ứng)
AMD = CNB (2 góc tương ứng) => 1800 - AMD = 1800 - CNB => AMN = CNM mà 2 góc này ở vị trí so le trong => AM // CN
=> AMCN là hình bình hành
=> AMCN là hình thoi
<=> AC _I_ BD
<=> ABCD là hình thoi
Bạn ơi vẽ giùm mình hình bài này với ạ <3