Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc ABM=góc CBM
=>góc ABM=góc AMB
=>ΔABM cân tại A
b: Xét ΔBAM và ΔDCN có
góc BAM=góc DCN
BA=DC
góc ABM=góc CDN
=>ΔBAM=ΔDCN
=>BM=DN và AM=CN
=>BN=DM
=>DMBN là hình bình hành

Bạn tự vẽ hình nhá!!!!
a) ABCD là hình bình hành=>góc ADC=góc ABC => góc MBN=góc MDN
Mà: góc MBN= góc BNC( so le trong) => góc BNC=góc MDN => DM//BN
b) Từ phần a ta có:
Xét DMNB có DM//BN
BM//DN (do AB//CD)
=> DMNB là hbh
c) Ta có:
góc AMD= góc MDC(so le trong) => góc ADM= góc AMD=> Tam giác AMD cân tại A
Mà: AH là đường phân giác=> AH là đường cao<=> AH vuông góc với DM (1)
=>AG vuông góc với BN ( do DM//BN) (2)
Tương tự, ta cũng chứng minh được tam giác BNC cân tại C
Mà: CF là đường PG=> CF vuông góc với BN (3)
Từ (1); (2); (3) => HEFG là hcn do có 3 góc vuông

a: Ta có: \(\widehat{ADE}=\dfrac{\widehat{ADC}}{2}\)
\(\widehat{CBF}=\dfrac{\widehat{CBA}}{2}\)
mà \(\widehat{ADC}=\widehat{CBA}\)
nên \(\widehat{ADE}=\widehat{CBF}\)
Xét ΔADE và ΔCBF có
\(\widehat{ADE}=\widehat{CBF}\)
AD=BC
\(\widehat{DAE}=\widehat{BCF}\)
Do đó: ΔADE=ΔCBF
Suy ra: AE=CF
Ta có: AE+EB=AB
CF+DF=CD
mà AB=CD
và AE=CF
nên EB=DF
Xét tứ giác DEBF có
EB//DF
EB=DF
Do đó: DEBF là hình bình hành
Suy ra: DE//BF
d: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
e: Ta có: ABCD là hình bình hành
nên Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường\(\left(1\right)\)
Ta có: EBFD là hình bình hành
nên Hai đường chéo EF và BD cắt nhau tại trung điểm của mỗi đường\(\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra AC,BD,EF đồng quy

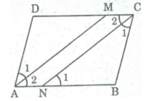
Ta có: ∠ A = ∠ C (tính chất hình bình hành)
∠ A 2 = 1/2 ∠ A ( Vì AM là tia phân giác của ∠ (BAD) )
∠ C 2 = 1/2 ∠ C ( Vì CN là tia phân giác của ∠ (BCD) )
Suy ra: ∠ A 2 = ∠ C 2
Do ABCD là hình bình hành nên AB // CD (gt)
Hay AN // CM (1)
Mà ∠ N 1 = ∠ C 2 (so le trong)
Suy ra: ∠ A 2 = ∠ N 1
⇒ AM // CN (vì có cặp góc ở vị trí đồng vị bằng nhau) (2)
Từ (1) và (2) suy ra tứ giác AMCN là hình bình hành.

https://www.google.com.vn/search?q=%C4%91%C3%A9o&source=lnms&tbm=isch&sa=X&ved=0ahUKEwjp8sz0oaTeAhVbUt4KHXc4AM0Q_AUIDigB&biw=1137&bih=723#imgrc=6ENXD-aPC-1TLM:
vào đó rồi mình làm cho
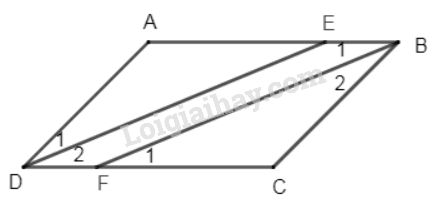
a) Vì ABCDABCD là hình bình hành (gt)
⇒ˆABC=ˆADC⇒ABC^=ADC^ (tính chất hình bình hành ) (1)
Vì BFBF là tia phân giác góc BB (gt)
⇒⇒ˆB1=ˆB2=ˆABC2B1^=B2^=ABC^2 (tính chất tia phân giác) (2)
Vì DEDE là tia phân giác góc DD (gt)
⇒⇒ ˆD1=ˆD2=ˆADC2D1^=D2^=ADC^2 (tính chất tia phân giác) (3)
Từ (1), (2), (3) ⇒ˆD2=ˆB1⇒D2^=B1^ mà hai góc này ở vị trí so le trong do đó: DE//BFDE//BF (*) (dấu hiệu nhận biết hai đường thẳng song song)
b) Ta lại có :ABCDABCD là hình bình hành (gt)
⇒⇒AB//CDAB//CD (tính chất hình bình hành) nghĩa là BE//DFBE//DF (**)
Từ (*) và (**) ta có tứ giác DEBFDEBF là hình bình hành (dấu hiệu nhận biết hình
a: Xét ΔADN và ΔCBM có
góc A=góc C
AD=CB
góc ADN=góc CBM
=>ΔADN=ΔCBM
b: ΔADN=ΔCBM
=>AN=CM
AN+NB=AB
CM+MD=CD
mà AN=CM và AB=CD
nên NB=MD
mà NB//MD
nên NBMD là hình bình hành
c: Xét tứ giác AMCN có
AN//CM
AN=CM
=>AMCN là hình bình hành