Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đầu bài chỗ " đường chéo BD cắt AE" chắc là " đường chéo BD cắt AI" phải không bn???
a) ta có: AB = CD ( ABCD là h.b.h)
=> AK = IC \(\left(=\frac{1}{2}AB=\frac{1}{2}CD\right)\)
mà AK // IC
=> AKCI là hình bình hành ( dấu hiệu)
xét \(\Delta DFC\)
có: DI =IC (gt)
EI // FC ( AKCI là h.b.h)
=> EI là đường trung bình của \(\Delta DFC\)
=> DE = EF ( t/c')
cmtt với \(\Delta AEB\)ta có: EF = FB
=> DE=EF=FB
b) xét \(\Delta ABD\)
có: AM=MD
AK=KB
=> KM là đường trung bình của \(\Delta ABD\)
=> KM // BD và \(KM=\frac{1}{2}BD\)
cmtt với \(\Delta BCD\)ta có: IN//BD và \(IN=\frac{1}{2}BD\)
=> KM // IN (//BD)
\(KM=IN\left(=\frac{1}{2}BD\right)\)
=> KMIN là hình bình hành ( dấu hiệu)

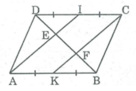
Ta có: AB = CD (tính chất hình bình hành)
AK = 1/2 AB (gt)
CI = 1/2 CD (gt)
Suy ra: AK = CI (1)
Mặt khác: AB // CD (gt)
⇒ AK // CI (2)
Từ (1) và (2) suy ra tứ giác AKCI là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
⇒ AI // CK
Trong ∆ ABE, ta có:
K là trung điểm của AB (gt)
AI // CK hay KF // AE nên BF = EF (tính chất đường trung bình tam giác)
Trong ∆ DCF, ta có:
I là trung điểm của DC (gt)
AI // CK hay IE // CF nên DE = EF (tính chất đường trung bình tam giác)
Suy ra: DE = EF = FB
Ta có: AB = CD (tính chất hình bình hành)
AK = 1/2 AB (gt)
CI = 1/2 CD (gt)
Suy ra: AK = CI (1)
Mặt khác: AB // CD (gt)
⇒ AK // CI (2)
Từ (1) và (2) suy ra tứ giác AKCI là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
⇒ AI // CK
Trong ∆ ABE, ta có:
K là trung điểm của AB (gt)
AI // CK hay KF // AE nên BF = EF (tính chất đường trung bình tam giác)

A B R D C I E F
ABCD là hình bình hành
=> AB // CD ; AB = CD (1)
K là trung điểm của AB
\(\Rightarrow KA=KB=\frac{AB}{2}\) (2)
I là trung điểm của CD
\(\Rightarrow ID=IC=\frac{CD}{2}\) (3)
Từ (1) , (2) , (3) => AK // CI ; AK = CI
=> AKCI là hình bình hành
=> AI // CK
Xét \(\Delta CDF\) có :
ID = IC
IE // CF ( AI // CK )
=> DE = EF
Xét \(\Delta ABE\) có :
KA = KB ( giả thiết )
KF // AE
=> BF = FE
=> DE = EF = FB

xét tứ giác AKCI có:AK=IC(vì AB=DC)
AI song song IC
\(\rightarrow\)AKCI là hbh
\(\rightarrow\)AI song song KC
xét tg DFC:DI=IC
EI song song FC
\(\rightarrow\)DE=EF(vì EI là đg tb) (1)
cm tương tự tg ABE\(\rightarrow\)EF=FB (2)
từ (1),(2)\(\Rightarrow\)DE=EF=FB

Giải :
a) + K là trung điểm của AB ⇒ AK = \(\frac{AB}{2}\).
+ I là trung điểm của CD ⇒ CI = \(\frac{CD}{2}\).
+ ABCD là hình bình hành
⇒ AB // CD hay AK // CI
và AB = CD ⇒ AB/2 = \(\frac{CD}{2}\) hay AK = CI
+ Tứ giác AKCI có AK // CI và AK = CI
⇒ AKCI là hình bình hành.
b) + AKCI là hình bình hành
⇒ AI // KC hay \(\frac{MI}{NC}\).
\(a)\)
\(K\)là trung điểm \(AB\)\(\Rightarrow AK=\frac{AB}{2}\)
\(I\)là trung điểm \(CD\)\(\Rightarrow CI=\frac{CD}{2}\)
Mà theo đề ra: \(ABCD\)là hình bình hành
\(\Rightarrow AB//CD\)hay \(AK//CI\)
\(\Rightarrow AB=CD\Rightarrow\frac{AB}{2}=\frac{CD}{2}\)hay \(AK=CI\)
Tứ giác \(AKCI\)có \(AK//CI\)\(;\)\(AK=CI\)
\(\Rightarrow AKCI\)là hình bình hành
\(b)\)
Theo phần a), ta có: \(AKCI\)là hình bình hành
\(\Rightarrow AI//KC\)hay \(MI//NC\)
A K B N M I C D

A B C D E F I J K
a)
ta có: ABCD là hình vuông
=> AB=BC=CD=DA=>1/2AB=1/2CD=AI=JC
AI//JC
=>tứ giác AICJ là hình bình hành
gọi trung điểm của AC là K
ta có:ABCD là hình vuông=> AC và BD cắt nhau tại trung điểm của mỗi đường
=>BD cắt AC tại K(1)
ta có AICJ là hình bình hành => AC và DJ cắt nhau tại trung điểm của mỗi đường
=>DJ cắt AC tại K(2)
từ (1)(2)=> 3 đoạn thẳng AC,BD,Ị cắt nhau tại trung điểm K của chúng
b)
ta có:
góc ADB=góc DBC
AJ//IC=> góc AED=góc CFB
ta có:
\(\widehat{EAD}=180^o-\widehat{ADB}-\widehat{AED}\)
\(\widehat{FCB}=180^o-\widehat{DBC}-\widehat{CFB}\)
=>góc EAD=góc FCB
xét tam giác DEA và tam giác BFC có
AD=BC(gt)
góc ADB=góc DBC
góc EAD=góc FCB(cmt)
=>tam giác DEA=tam giác BFC(g.c.g)
=>AE=CF
c)
ta có:tứ giác AICJ là hình bình hành
=>AJ=IC
AE=CF
EJ=AJ-AE
IF=IC-FC
=>EJ=IF
EJ//IF
=>tứ giác IFJE là hình bình hành
d)
xét tam giác ACD có
DK là trung tuyến ứng với cạnh AC
AJ là trung tuyến ứng với cạnh CD
=>giao của DK và AJ là trọng tâm tam giác ACD
=>E là trọng tâm tam giác ACD
cm tương tự ta có: F là trọng tâm tam giác ABC
ta có:
E là trọng tâm tam giác ADC
=>EK=1/2DE
F là trọng tâm tam giác ABC
=>FK=1/2BF
DE=BF(tam giác DEA=tam giác BFC)
=>EK=FK
ta có:
=>FB= DE=2EK=EK+KF=EF
=>DE=EF=FB(đfcm)

a: Xét tứ giác AICK có
AK//CI
AK=CI
Do đó: AICK là hình bình hành
Kiểm tra lại đề!
Bạn lại đùa mình rồi :))) giúp ngta đi chứ :>
ăn ở "tốt" quá thôi :)) hnay onl mà chẳng vào trả lời lười ghiaaa