Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham Khảo Nha :
Xét hbh ABCD có :
AB = CD; AB // CD
Mà e là trg điểm của AB, E là trg điểm của CD
=> AF//EC, AF=EC
=> Tứ giác AFEC là hbh
b/ Xét tam giác DHC có:
IE//HC( hbh AFEC)
E là trg điểm của DC
=> I là trg điểm của DH (1)
chứng minh tương tự tam giác AIB
=> H là trg điểm của IB (2)
Từ (1) và (2) => đpcm
c/Xét tam giác DHC có:
I là ttrg điểm của DH
E là trg điểm của DC
=> IE là đg trbình của tg DHC
=> IE= 1/2 HC (3)
Xeý tg IEB có:
H là trg điểm của IB
HJ // IE (AE// FC; J thuộc FC)
=> J là trung điểm của BE
=> HJ là đg trbình của tg BIE
=> HJ = 1/2 IE (4)
Từ (3) và (4) => HJ = 1/4 HC hay 4HJ = HC
A B C D F I H E J
a, Xét tứ giác AECF có:
AF = CE ( AB = CD )
AF // CE ( AB // CD )
=> AECF là hình bình hành ( đpcm )
b, Xét \(\Delta ABI\) có:
F là trung điểm AB (gt)
AI // FH ( AE // CF )
=> FH là đg trung bình của \(\Delta ABI\)
=> HI = HB (1)
C/m tương tự ta có: EI là đg trung bình \(\Delta CDH\)
=> HI = HD (2)
Từ (1) và (2) => DI = IH = HB ( đpcm )
Bn tham khảo nhé, câu c mk chưa nghĩ ra, thấy bn đg gấp mà
Hok tốt

b: Xét tứ giác AFEC có AF//EC và AF=EC
nên AFEC là hình bình hành
Xét ΔDHC có
E là trung điểm của DC
EI//HC
Do đó: I là trung điểm của DH
Xét ΔBAI có
F là trung điểm của BA
FH//AI
Do đó: H la trung điểm của BI
=>DI=IH=HB
c: Vì BFEC là hình bình hành
nên BE cắt FC tại trung điểm của mỗi đường
=>H là trung điểm chung của BE và CF
Xét ΔBIE có BJ/BI=BH/BE
nên JH/IE=1/2
=>JH=1/2IE
Xét ΔDHC có DE/DC=DI/DH
nên EI//HC và EI=1/2HC
=>JH=1/4HC
=>HC=4JH

a) Vì ABCD là hình bình hành
=> AB//CD hay AE//CF (1)
+) AB = CD ( vì là 2 cạnh đối)
=> 1/2 AB= 1/2 CD
=> AE = CF (2)
Từ (1) và (2)
=> 2 cạnh đối AE và CF song song và bằng nhau
=> tứ giác AECF là hình bình hành
Mk mới làm đc phần a thôi h mk bận r có j ib mk giải cho nha !!!
Xin lỗi bạn nhiều !!

a,Vi ABCD la hbh(gt)
=>AB=CD;AB//CD
Ma M€AB;N€CD
=>MB//ND
Vi M la trung diem cua AB
=>MA=MB=AB/2
Vi N la trung diem cua CD
=>CN=ND=CD/2
Ma AB=CD(cmt)
=>MB=DN
Tg DMBN co:
MB//DN(cmt)
MB=ND(cmt)
=>Tg DMBN la hbh(dh)

Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành

A E F N B C M D
do ABCD là hình bình hành
=>AD//BC
=>\(\widehat{DAC}=\widehat{BCA}\)(so le)
Xét \(\Delta ADE\) và \(\Delta CBF\) có:
AD=BC( do ABCD là hình bình hành)
\(\widehat{DAC}=\widehat{BCA}\)(cmt)
AE=CF(gt)
=>\(\Delta ADE\)=\(\Delta CBF\)(c.g.c)
=>\(\widehat{AED}=\widehat{CFB}\)
Ta có:
\(\widehat{AED}=\widehat{NEC}(đối dỉnh) \)
\(\widehat{BFC}=\widehat{AFM}(đối đỉnh)\)
=>\(\widehat{NEC}=\widehat{AFM}\)
Mà hai góc này ở vị trí so le trong
=>DN//MB
=>EN//BF(1)
Lại có:
AE=EF(2)
=>AN=NB=> N là trung điểm của AB
MB//DN=>MF//DE(3)
Lại có: CF=EF(4)
Từ (3),(4)
=>CM=MD
=> M là trung điểm của CD

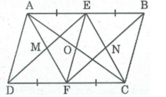
+) Ta có:
AE = 1/2 AB; CF = 1/2. CD ( vì E và F lần lượt là trung điểm của AB, CD).
Và AB = CD (tính chất hình bình hành)
Suy ra: AE = CF
+) Lại có: AB // CD ( vì ABCD là hình bình hành) nên AE //CF
Tứ giác AECF có hai cạnh đối AE, CF song song và bằng nhau nên là hình bình hành
⇒ AF //CE hay EN // FM (1)
Xét tứ giác BFDE ta có:
AB // CD (gt) hay BE // DF
BE = 1/2 AB (gt)
DF = 1/2 CD (gt)
AB = CD (tính chất hình bình hành)
Suy ra: BE = DF
Tứ giác BFDE là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau) ⇒ BF//DE hay EM // FN (2)
Từ (1) và (2) suy ra tứ giác EMFN là hình bình hành (theo định nghĩa hình bình hành)