Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bằng \(\overrightarrow{AB}\) là \(\overrightarrow{DC}\)
Bằng \(\overrightarrow{OB}\) là \(\overrightarrow{DO}\)
Có độ dài bằng OB là \(\overrightarrow{OB};\overrightarrow{BO};\overrightarrow{OD};\overrightarrow{DO}\)
a) Bằng vectơ AB :
\(\overrightarrow{DC}\)
Bằng vectơ OB :
\(\overrightarrow{DO}\)
b)Có độ dài bằng OB :
\(\overrightarrow{OD},
\overrightarrow{DO},
\overrightarrow{BO}\)

A B C D O M N
a)
Các véc tơ cùng phương với \(\overrightarrow{AB}\) là:
\(\overrightarrow{MO};\overrightarrow{OM};\overrightarrow{MN};\overrightarrow{NM};\overrightarrow{NO};\overrightarrow{ON};\overrightarrow{DC};\overrightarrow{CD};\overrightarrow{BA};\overrightarrow{AB}\).
Hai véc tơ cùng hướng với \(\overrightarrow{AB}\) là:
\(\overrightarrow{MO};\overrightarrow{ON}\).
Hai véc tơ ngược hướng với \(\overrightarrow{AB}\) là:
\(\overrightarrow{OM};\overrightarrow{ON}\).
b) Một véc tơ bằng véc tơ \(\overrightarrow{MO}\) là: \(\overrightarrow{ON}\).
Một véc tơ bằng véc tơ \(\overrightarrow{OB}\) là: \(\overrightarrow{DO}\).


Do C đối xứng A qua B nên B là trung điểm AC
Áp dụng công thức trung điểm:
\(\left\{{}\begin{matrix}x_B=\frac{x_A+x_C}{2}\\y_B=\frac{y_A+y_C}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_C=2x_B-x_A=7\\y_C=2y_B-y_A=2\end{matrix}\right.\) \(\Rightarrow C\left(7;2\right)\)
\(\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{AB}+\overrightarrow{OD}+\overrightarrow{DC}=\overrightarrow{AB}+\overrightarrow{DC}=3\overrightarrow{DC}\)
\(\Rightarrow\left|\overrightarrow{OB}+\overrightarrow{OC}\right|=3\left|\overrightarrow{DC}\right|=3a\)
Câu c cần biểu diễn vecto DE theo 2 vecto nào bạn?

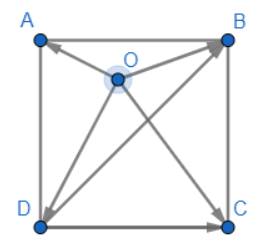
Ta có: \(AB = BC = CD = DA = 1;\)
\(AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{1^2} + {1^2}} = \sqrt 2 \)
a) \(\overrightarrow a = \overrightarrow {OB} - \overrightarrow {OD} = \overrightarrow {OB} + \overrightarrow {DO} = \left( {\overrightarrow {DO} + \overrightarrow {OB} } \right) = \overrightarrow {DB} \)
\( \Rightarrow \left| {\overrightarrow a } \right| = \left| {\overrightarrow {DB} } \right| = DB = \sqrt 2 \)
b) \(\overrightarrow b = \left( {\overrightarrow {OC} - \overrightarrow {OA} } \right) + \left( {\overrightarrow {DB} - \overrightarrow {DC} } \right)\)
\( = \left( {\overrightarrow {OC} + \overrightarrow {AO} } \right) + \left( {\overrightarrow {DB} + \overrightarrow {CD} } \right) = \left( {\overrightarrow {AO} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {CD} + \overrightarrow {DB} } \right)\)
\( = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \)
\( \Rightarrow \left| {\overrightarrow b } \right| = \left| {\overrightarrow {AB} } \right| = AB = 1\)
Chú ý khi giải:
Khi có dấu trừ phía trước ta thường thay bằng vectơ đối của nó và ngược lại
a: vecto DC=vecto AB
vecto OB=vecto DO
b: \(\left|\overrightarrow{OD}\right|=\left|\overrightarrow{OB}\right|\)