Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S A B C = 1/3 S A B C D = S/2
CN = 1/3 BC , NT // AB.
Theo tính chất đường thẳng song song cách đều ⇒ CT = 1/3 AC
△ ABC và △ BTC có chung chiều cao kẻ từ đỉnh B, đáy CT = 1/3 AC
⇒ S B T C = 1/3 S A B C = 1/3 . S/2 = S/6
△ BTC và △ TNC có chung chiều cao kẻ từ đỉnh T, cạnh đáy CN = 1/3 CB
⇒ S T N C = 1/3 S B T C = 1/3 . S/6 = S/18
S A B N T = S A B C - S T N C = S/2 - S/18 = 9S/18 - S/18 = 4S/9

△ DMC có CM = 2/3BC
Hình bình hành ABCD và ΔDMC có chung đường cao kẻ từ đỉnh D đến BC.
Gọi độ dài đường cao là h, BC = a
Ta có diện tích hình bình hành ABCD là S = a h
S D M C = 1/2 h. 2/3 a = 1/3 ah = 1/3 S
S A B M D = S A B C D - S D M C = s - 1/3 S = 2/3 S

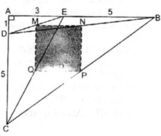
A P B C N Q M
+) AP // BC => S ( BCP ) = S ( BAC ) = S (1)
+) AP //BC => Theo talet: \(\frac{PN}{NM}=\frac{AN}{NC}=\frac{1}{2}\)( vì AC = 3AN )
Theo menelaus xét trong tam giác PMC
\(\frac{CQ}{PQ}.\frac{NP}{NM}.\frac{BM}{BC}=1\)=> \(\frac{CQ}{PQ}.\frac{1}{2}.\frac{1}{3}=1\)=> CQ = 6PQ => CP = 7 QP
=> \(\frac{S\left(QPB\right)}{S\left(CPB\right)}=\frac{QP}{CP}=\frac{1}{7}\)
=> S ( QPB ) = S/7
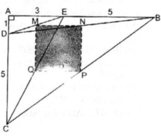
A B C M I D N Q
Có AB//PM => \(\frac{PI}{IB}=\frac{IN}{IA}\left(1\right)\)
Có AD//BC \(\Rightarrow\frac{DI}{IB}=\frac{IA}{IC}\left(2\right)\)
Từ (1)(2) => \(\frac{IN}{IA}=\frac{IA}{IC}\Rightarrow IA^2=IN\cdot IC\)
Xét \(\Delta PMC\) cắt tuyến BQ. Áp dụng Menelaus
\(\Rightarrow\frac{PQ}{QC}\cdot\frac{CB}{BM}\cdot\frac{MN}{NP}=1\)
\(\Leftrightarrow\frac{PQ}{QC}\cdot\frac{3}{1}\cdot\frac{2}{1}=1\Rightarrow\frac{PQ}{QC}=\frac{1}{6}\Rightarrow\frac{PQ}{PC}=\frac{1}{7}\)
Có \(S_{ABC}=S_{PBC}\Rightarrow S_{PBQ}=\frac{1}{7}S=\frac{S}{7}\)


A B C D M N T h
a) dt(ABMD) = dt(ABCD) - dt(CMD)
Mà dt(CMD) = 1/2 MC.h = 1/2 . 2/3 . BC .h = 1/3 dt(ABCD) = 1/3.S
(với h là đường cao hạ từ A xuống BC của hình bình hành ABCD)
Suy ra dt(ABMD) = S - 1/3 S = 2/3. S
b) dt(ABNT) = BN.h = 2/3 BC . h = 2/3 . S