Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Trong đường tròn nhỏ:
AB > CD => OH < OK (định lí 3)
b) Trong đường tròn lớn:
OH < OK => ME > MF (định lí 3)
c) Trong đường tròn lớn:
ME > MF => MH > MK

a) Trong đường tròn nhỏ:
AB > CD => OH < OK (định lí 3)
b) Trong đường tròn lớn:
OH < OK => ME > MF (định lí 3)
c) Trong đường tròn lớn:
ME > MF => MH > MK
a) Xét trong đường tròn nhỏ:
Theo định lí 22: trong hai dây của một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn.
Theo giả thiết AB>CDAB>CD suy ra ABAB gần tâm hơn, tức là OH<OKOH<OK.
b) Xét trong đường tròn lớn:
Theo định lí 22: trong hai dây của một đường tròn, dây nào gần tâm hơn thì dây đó lớn hơn.
Theo câu aa, ta có: OH<OK⇒ME>MFOH<OK⇒ME>MF.
c) Xét trong đường tròn lớn:
Vì OH⊥ME⇒EH=MH=ME2OH⊥ME⇒EH=MH=ME2 (Định lý 2 - trang 103).
Vì OK⊥MF⇒KF=MK=MF2OK⊥MF⇒KF=MK=MF2 (Định lý 2 - trang 103).
Theo câu bb, ta có: ME>MF⇒ME2>MF2⇔MH>MK

| Vị trí tương đối của hai đường tròn | Số điểm chung | Hệ thức giữa d,R,r |
| (O,R) dựng (O’,r’) | 0 | D<R-r |
| (O;R) ở ngoài nhau (O’;r) | 0 | D>R+r |
| Tiếp xúc ngoài | 1 | D=R+r |
| Tiếp xúc trong | 1 | D=R-r |
| Hai đường tròn cắt nhau | 2 | R-r<d<R+r |
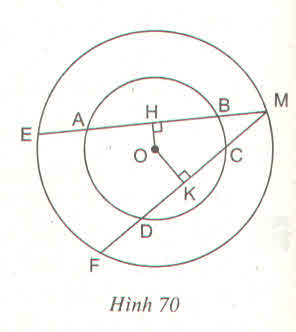




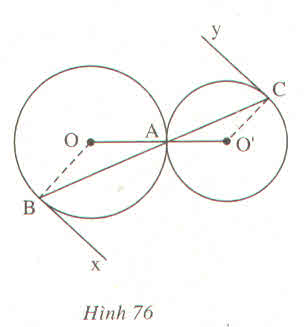


a) Xét đường tròn nhỏ ta được OH<OKOH<OK.
b) Xét đường tròn lớn ta được ME>MFME>MF.
c) Từ kết quả câu b) suy ra MH>MKMH>MK.