Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

giải
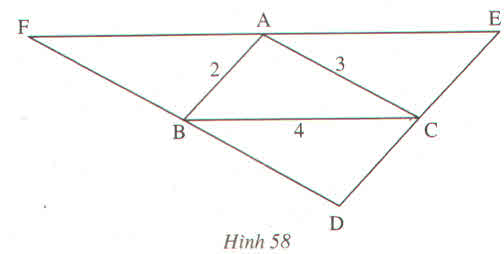
*xét tam giác abc và tam giác abf có
góc abc=góc bà(so le trong)
ad;chung
góc bac=góc abf(so le trong)
suy ra tam giác abc=tam giác abf(gcg)
suy ra af=bc=4(2 cạnh tương ứng)
bf=ac=3
*xét tam giác abc và tam giác ace có
góc acb=góc cae(số lẻ trong)
ac; chung
gốc bac= gốc eca(slt)
suy ra tam giác abc= tam giác ace
suy ra ae=bc=4(2 cạnh tương ứng)
ce=ab=2
* xét tam giác abc và tam giác dcb có
góc acb= góc dbc(slt)
bc;chung
góc abc= góc dcb
suy ra tam giác abc=tam giác dcb
suy ra dc=ab=2
db=ac=3
ta có ef=ae+af=4+4=8
df=db+bf=3+3=6
de=dc+ce=2+2=4
vậy chu vi của tam giác def là
để+DF+EF=4+6+8=18(ĐƠN VỊ ĐO ĐỘ DÀI)

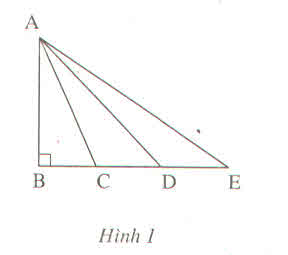
Điểm C nằm giữa B và D nên BC < BD (1)
Điểm C nằm giữa B và E nên BD < BE (2)
Vì B, C, D, E thẳng hàng. Từ (1) và (2) suy ra
BC < BD < BE
AB⊥BE
Suy ra: AB < AC < AD < AE.

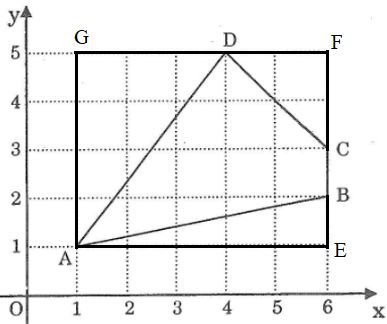
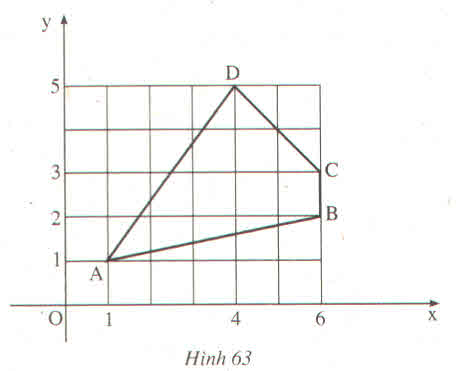
Ta có: \(BC=1.\)
+ Xét \(\Delta ABE\) vuông tại E có:
\(AB^2=AE^2+BE^2\) (định lí Py - ta - go).
=> \(AB^2=5^2+1^2\)
=> \(AB^2=25+1\)
=> \(AB^2=26\)
=> \(AB=\sqrt{26}\) (vì \(AB>0\)).
+ Xét \(\Delta CDF\) vuông tại F có:
\(CD^2=DF^2+CF^2\) (định lí Py - ta - go).
=> \(CD^2=2^2+2^2\)
=> \(CD^2=4+4\)
=> \(CD^2=8\)
=> \(CD=\sqrt{8}\) (vì \(CD>0\)).
+ Xét \(\Delta ADG\) vuông tại G có:
\(AD^2=AG^2+DG^2\) (định lí Py - ta - go).
=> \(AD^2=4^2+3^2\)
=> \(AD^2=16+9\)
=> \(AD^2=25\)
=> \(AD=5\) (vì \(AD>0\)).
Vậy \(AB=\sqrt{26};BC=1;CD=\sqrt{8};AD=5.\)
Chúc bạn học tốt!
Ta tính được : AB = \(\sqrt{26}\) ; CD = \(\sqrt{8}\) ; BC = 1 ; DA = 5

Ta có: AB > AC (gt)
Suy ra: HB > HC (đường xiên lớn hơn có hình chiếu lớn hơn)
Suy ra: EB > EC (hình chiếu lớn hơn thì có đường xiên lớn hơn)

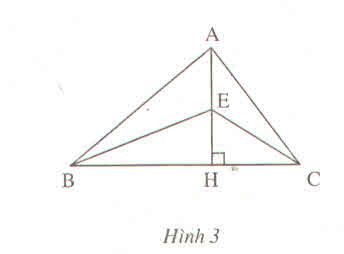
a) △ABC có : Hai đường cao BE và AD mà 2 đường này cùng cắt nhau tại điểm I ⇒ I là trực tâm
⇒ CI là đường cao còn lại ⇒ CI ⊥ AB
b) Xét △BEC có : góc EBC + gócBEC + góc BCE = \(180^0\)( định lí tổng ba góc )
⇒ góc EBC = \(180^0\) - góc BEC - góc BCE = \(180^0\)- \(90^0\)-\(40^0\)= \(50^0\)
Lại xét △BID có : góc BID + góc IBD + góc BDI = \(180^0\)
⇒ góc BID = \(180^0\) - \(90^0\) - \(50^0\) = \(40^0\)
Có góc BID + góc DIE = \(180^0\)( 2 góc kề bù )
⇒ góc DIE = \(180^0\) - góc BID = \(180^0-40^0\)= \(140^0\)

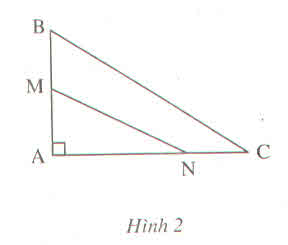
Hình chiếu của AN < hình chiếu của AC
=> đường xiên BN < đường xiên của BC (1)
Hình chiếu của AM < hình chiếu AB => đường xiên MN < đường xiên NB. (2)
Từ (1) và (2) suy ra:
MN< BN< BC.


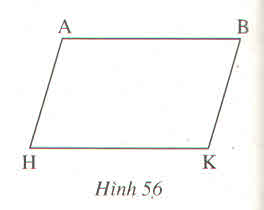
Nối A với K
Xét tam giác ABK và tam giác AHK có:
AK: cạnh chung
góc BAK = góc AKH (AB // HK)
góc HAK = góc AKB (AH //BK)
=> tam giác ABK = tam giác AHK
=> AB = HK (hai cạnh tương ứng)
Ta có: tam giác ABK = tam giác AHK
=> AH = BK (hai cạnh tương ứng)
kẻ đoạn thẳng AK
Xét tamgiác KAH và tam giác AKB
góc HAK = góc BKA (2 góc so le trong do AK cắt AH// BK )
cạnh AK chung
góc HKA = góc BAK (2 góc so le trong do AB //HK )
=> tam giác KAH = tam giác AKB ( g.c.g.)
=> AB=HK (2 cạnh tương ướng )
=> AH = BK (2 cạnh tương ướng )
đúng không..............................................
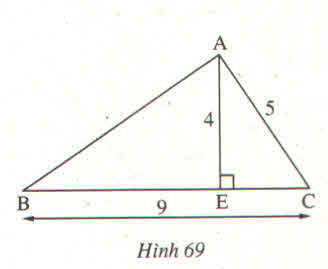







Tam giác AEC có góc AEC = \(90^0\)
=> \(AC^2=AE^2+EC^2\)
=>\(EC^2=AC^2-AE^2\)
=>\(EC^2=5^2-4^2\)
=>\(EC=\sqrt{9}=3\left(m\right)\)
Có EB + EC = BC
=>EB = BC - EC
=>EB = 9 - 3
=> EB = 6 (m)
Tam giác AEB có góc AEB = \(90^0\)
=>\(AB^2=AE^2+EB^2\)
=>\(AB^2=4^2+6^2\)
=>\(AB^2=16+36\)
=>\(AB^2=52\)
=>\(AB=\sqrt{52}=2\sqrt{13}\) (m)