Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) △ABC có : Hai đường cao BE và AD mà 2 đường này cùng cắt nhau tại điểm I ⇒ I là trực tâm
⇒ CI là đường cao còn lại ⇒ CI ⊥ AB
b) Xét △BEC có : góc EBC + gócBEC + góc BCE = \(180^0\)( định lí tổng ba góc )
⇒ góc EBC = \(180^0\) - góc BEC - góc BCE = \(180^0\)- \(90^0\)-\(40^0\)= \(50^0\)
Lại xét △BID có : góc BID + góc IBD + góc BDI = \(180^0\)
⇒ góc BID = \(180^0\) - \(90^0\) - \(50^0\) = \(40^0\)
Có góc BID + góc DIE = \(180^0\)( 2 góc kề bù )
⇒ góc DIE = \(180^0\) - góc BID = \(180^0-40^0\)= \(140^0\)

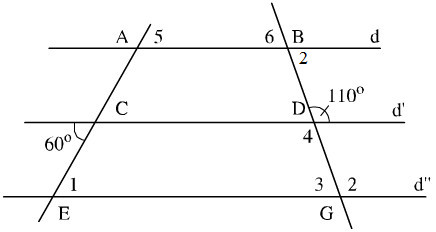
Xem hình vẽ. Có thể tính bằng nhiều cách, chẳng hạn:
+Vì d’ //d’’ có: \(\widehat{E}_1\) và góc 600 là hai góc so le trong nên \(\widehat{E}_1\)= 600
+Vì d’ // d’’ có: \(\widehat{G}_2\)và góc 1100 là hai góc đồng vị nên \(\widehat{G_2}\) = 1100
+ \(\widehat{G}_2\)+\(\widehat{G}_3\)=\(180^0\) (hai góc kề bù)
Nên \(\widehat{G_3}=180^0-\widehat{G}_2=180^0-110^0=70^0\)
+) \(\widehat{D}_4\)1100 (vì là hai góc đối đỉnh)
+) \(\widehat{A}_5\) = \(\widehat{A}_1\) (Hai góc đối đỉnh)
Mà \(\widehat{A}_1\)= 600 (vì là hai góc đồng vị)
Nên \(\widehat{A}_5\) = 600 .
+ \(\widehat{B}_6\) = \(\widehat{B}_2\)(vì là hai góc đối đỉnh)
Mà \(\widehat{B}_2\) + 1100 = 1800 (hai góc trong cùng phía)
Nên \(\widehat{B}_2\) = 1800 - 1100 = 700.
Do đó: \(\widehat{B}_6\) = 700
a) Năm cặp đường thẳng vuông góc là:
d3 ⊥ d4; d3 ⊥ d5; d3 ⊥ d7; d1 ⊥ d8; d1 ⊥ d2
b) Bốn cặp đường thẳng song song là: d4//d5; d5//d7; d4//d7; d8//d2

đây là cậu chép trg chỗ giải đáp rồi mà mk ko đc lm giống trg giải đáp

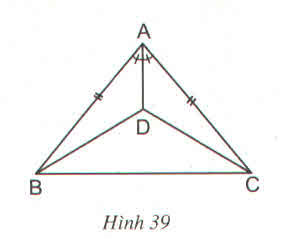
a) Căn cứ các kí hiệu đã cho trên hình của bài 39 ta có: ∆ABD và ∆ACD có:
AB = AC
ˆBAD=ˆCADBAD^=CAD^
AD là cạnh chung
=> ∆ABD = ∆ACD
b) Vì ∆ABD = ∆ACD
=> BD = CD => ∆BCD cân tại D
=> ˆDBC=ˆDCB
Hướng dẫn:
a) ∆KIL có ˆII^ = 620
nên ˆIKL+ˆILKIKL^+ILK^ = 1180
Vì KO và LO là phân giác ˆIKLIKL^, ˆILKILK^
nên ˆOKL+ˆOLKOKL^+OLK^= 1212(ˆIKL+ˆILKIKL^+ILK^)
=> ˆOKL+ˆOLKOKL^+OLK^ = 1212 1180
ˆOKL+ˆOLKOKL^+OLK^ = 590
∆KOL có ˆOKL+ˆOLKOKL^+OLK^ = 590
nên ˆKOLKOL^ = 1800 – 590 = 1210

c) Vì O là giao điểm của hai đường phân giác của ˆKK^ và ˆLL^ nên O cách đều ba cạnh của tam giác IKL
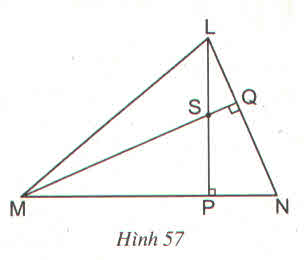










a) Từ hình vẽ ta có: LP ⊥ MN; MQ ⊥ LN
ΔMNL có S là giao điểm của hai đường cao LP và MQ nên S chính là trực tâm của tam giác (định lí ba đường cao).
=> NS cũng là đường cao trong tam giác hay NS ⊥ LM (đpcm).
b) ΔNMQ vuông tại Q có góc LNP = 50o nên góc QMN = 40o
ΔMPS vuông tại P có góc QMP = 40o nên góc MSP = 50o
Vì hai góc MSP và PSQ là hai góc kề bù nên suy ra:
góc PSQ = 180o - 50o = 130o.
Hướng dẫn:
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay
SN ⊥ ML
b) ∆NMQ vuông tại Q có ˆLNPLNP^ =500 nên ˆQMNQMN^ =400
∆MPS vuông tại Q có ˆQMPQMP^ =400 nên ˆMSPMSP^ =500
Suy ra ˆPSQPSQ^ =1300(kề bù)